1.1. Линейные модели ¶

Ниже приводится наборы методов линейных моделей, предназначенные для регрессии, в которых целевое значение ожидается как линейная комбинация функций. В математической записи, если $\hat{y}$ прогнозируемое значение.
$$\hat{y}(w, x) = w_0 + w_1 x_1 + … + w_p x_p$$

В моделе мы получаем вектор  $w = (w_1, …, w_p)$  как coef_ и $w_0$ как intercept_

Чтобы выполнить класификацию с помощью обобщенных линейных моделей, смотри раздел Логистическая регрессия

Обычный метод наименьших квадратов (Ordinary Least Squares, OLS) МНК

Линейная регрессия подгоняет линейную модель с коэффицентами $w = (w_1, … , w_p)$ к минимизации остаточной суммы квадрата между наблюдаемого целевого признака в наборе данных и предсказанно целевого признака по линейной аппроксимации. Математически это решение проблемы в следующем виде:

$$\min_{w} || X w — y||_2^2$$

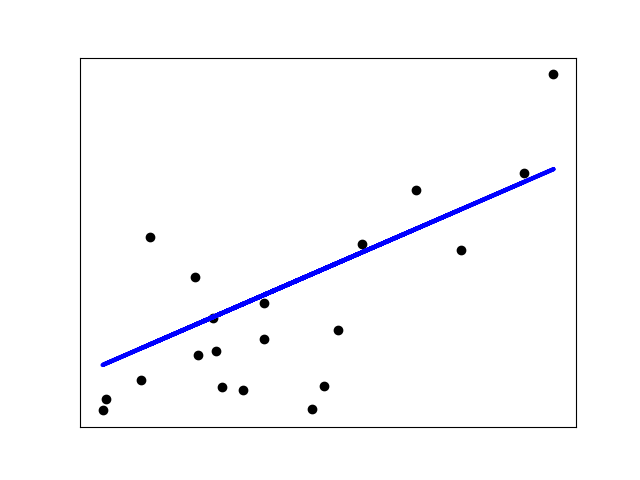
Метод LinearRegression имеет метод fit который принимает матрицу X и целевой признак y и будет хранить коэффиценты $w$ линейной модели в перменной coef_:

>>> from sklearn import linear_model 
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2]) 
LinearRegression() 
>>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2]) 
LinearRegression() 
>>> reg.coef_ array([0.5, 0.5])

Оценки коэффициентов для обыкновенных наименьших квадратов полагаются на независимость функций. Когда функции коррелированы и столбцы матрицы плана имеют приблизительную линейную зависимость, матрица плана становится близкой к сингулярной, и в результате оценка методом наименьших квадратов становится очень чувствительной к случайным ошибкам в наблюдаемой цели, что приводит к большой дисперсии. Эта ситуация мультиколлинеарности может возникнуть, например, когда данные собираются без экспериментального плана.

1.1.1.2. Сложность обыкновенных наименьших квадратов

Решение методом наименьших квадратов вычисляется с использованием разложения X по сингулярным числам. Если X является матрицей формы ( $n_{\text{samples}}$, $n_{\text{features}}$ ), этот метод имеет стоимость $O(n_{\text{samples}} n_{\text{features}}^2)$ , при условии, что $n_{\text{samples}} \geq n_{\text{features}}$. $$\min_{w} || X w — y||_2^2 + \alpha ||w||_2^2$$

Параметр сложности $\alpha \geq 0$ управляет степенью усадки: чем больше значение, тем больше величина усадки, и, таким образом, коэффициенты становятся более устойчивыми к коллинеарности.

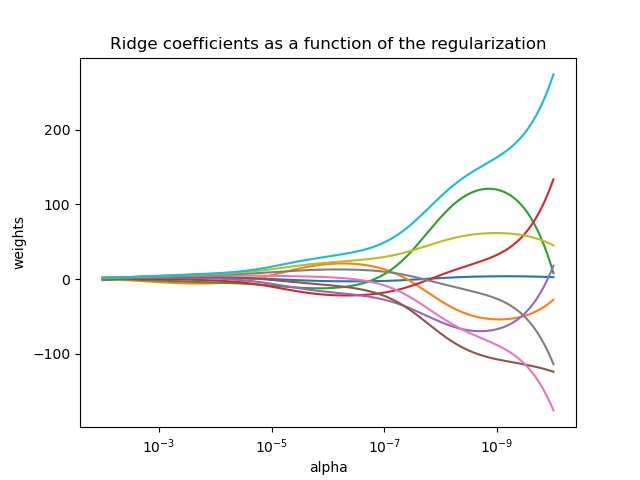
Как и в случае с другими линейными моделями, Ridge примет свой метод fit к массивам подбора X, y и сохранит коэффициенты линейной модели в своем члене coef_:

>>> from sklearn import linear_model
>>> reg = linear_model.Ridge(alpha=.5)
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5)
>>> reg.coef_
array([0.34545455, 0.34545455])
>>> reg.intercept_
0.13636...

1.1.2.2. Классификация

У регрессора Ridge есть вариант классификатора: RidgeClassifier. Этот классификатор сначала преобразует двоичные цели в {-1, 1}, а затем обрабатывает проблему как задачу регрессии, оптимизируя ту же цель, что и выше. Предсказанный класс соответствует знаку прогноза регрессора. Для мультиклассовой классификации проблема рассматривается как регрессия с несколькими выходами, и предсказанный класс соответствует выходу с наивысшим значением.

Может показаться сомнительным использование (штрафных) потерь по методу наименьших квадратов для соответствия классификационной модели вместо более традиционных логистических или шарнирных потерь. Однако на практике все эти модели могут приводить к одинаковым оценкам перекрестной проверки с точки зрения точности или точности / полноты, в то время как штрафные потери наименьших квадратов, используемые RidgeClassifier, позволяют совершенно разный выбор числовых решателей с различными профилями вычислительной производительности.

RidgeClassifier может быть значительно быстрее, чем, например, LogisticRegression с большим количеством классов, потому что он может вычислять матрицу проекции $(X^T X)^{-1} X^T$ только один раз.

Этот классификатор иногда называют машинами опорных векторов наименьших квадратов с линейным ядром.

Этот метод имеет тот же порядок сложности, что и обычный метод наименьших квадратов.

1.1.2.4. Настройка параметра регуляризации: перекрестная проверка с исключением одного-одного

RidgeCV реализует регрессию гребня со встроенной перекрестной проверкой альфа-параметра. Объект работает так же, как GridSearchCV, за исключением того, что по умолчанию используется перекрестная проверка Leave-One-Out:

>>> import numpy as np
>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=np.logspace(-6, 6, 13))
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
RidgeCV(alphas=array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
      1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06]))
>>> reg.alpha_
0.01

Указание значения атрибута cv вызовет использование перекрестной проверки с помощью GridSearchCV, например cv = 10 для 10-кратной перекрестной проверки, а не перекрестной проверки с оставлением одного значения.

References

1.1.3. Лассо

Лассо — это линейная модель, которая оценивает разреженные коэффициенты. Это полезно в некоторых контекстах из-за своей тенденции отдавать предпочтение решениям с меньшим количеством ненулевых коэффициентов, эффективно уменьшая количество функций, от которых зависит данное решение. По этой причине лассо и его варианты являются фундаментальными для области сжатого зондирования. При определенных условиях он может восстановить точный набор ненулевых коэффициентов (см. Компрессионное зондирование: реконструкция томографии с предварительным L1 (лассо)).

Математически он состоит из линейной модели с добавленным членом регуляризации. Целевая функция, которую необходимо минимизировать: $$\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w — y||_2 ^ 2 + \alpha ||w||_1}$$

Таким образом, оценка лассо решает проблему минимизации штрафа методом наименьших квадратов с помощью $\alpha ||w||_1$ добавлено, где $\alpha$ — постоянная, а $||w||_1$ это $\ell_1$-норма вектора коэффициентов.

Реализация в классе Lasso использует координатный спуск в качестве алгоритма подбора коэффициентов. См. Другую реализацию в разделе «Регрессия наименьшего угла»:

>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha=0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1)
>>> reg.predict([[1, 1]])
array([0.8])

Функция lasso_path полезна для задач нижнего уровня, поскольку она вычисляет коэффициенты по всему пути возможных значений.

Следующие две ссылки объясняют итерации, используемые в соревете координатного спуска Scikit-Suart, а также вычисления пробелов двойственности, используемые для контроля конвергенции.

1.1.3.1. Настройка параметра регуляризации

Параметр alpha контролирует степень потенциальности предполагаемых коэффициентов.

1.1.3.1.1. Использование крос валидации

scikit-learn обнажает объекты, которые устанавливают параметр Lasso Alpha путем перекрестной проверки: lassocv и lassolarscv. Lassolarscv основан на алгоритме регрессии наименьших углов, объясненных ниже.

Для высокомерных наборов данных с множеством коллинеарных особенностей Lassocv чаще всего предпочтительнее. Тем не менее, Lassolarscv имеет преимущество в изучении более актуальных значений альфа-параметра, и если количество образцов очень мало по сравнению с количеством функций, он часто быстрее, чем Lassocv.

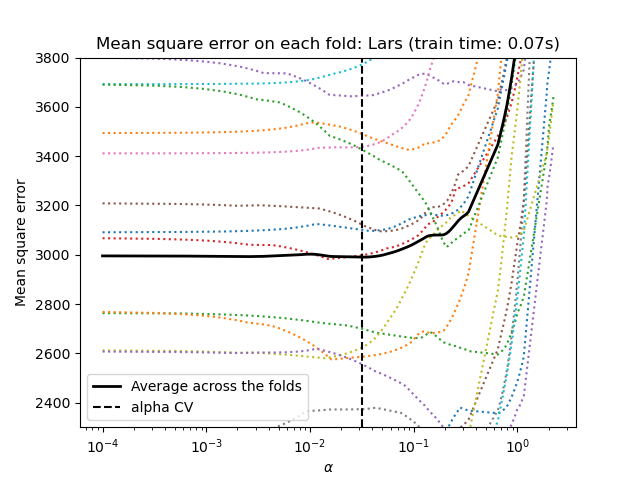
1.1.3.1.2. Выбор моделей на основе информационно-критериев

Альтернативно, оценщика Lassolarsic предлагает использовать информационный критерий (AIC AIC) и информационный критерий Bayes (BIC). Это вычислительная более дешевая альтернатива находить оптимальное значение альфа в качестве пути регуляризации, вычисляется только один раз вместо k + 1 раза при использовании кросс-проверки K-Fold. Однако такие критерии нуждаются в надлежащей оценке степеней свободы решения, получены для больших образцов (асимптотических результатов) и предполагают, что модель является правильной, то есть, что данные фактически генерируются этой моделью. Они также имеют тенденцию ломаться, когда проблема плохо обусловлена (больше особенностей, чем образцов).

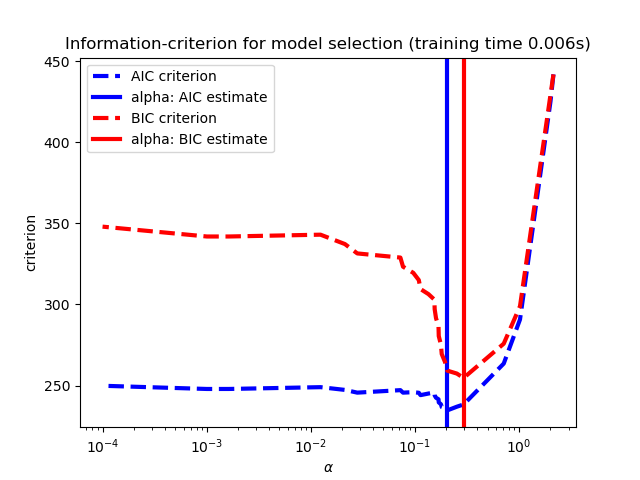
1.1.3.1.3. Сравнение с параметром регуляризации SVM

Эквивалентность между альфам и параметром регуляризации SVM, C с помощью alpha = 1 / C или alpha = 1 / (n_samples * C), в зависимости от оценки и точной объективной функции, оптимизированной моделью.

1.1.4. Мультизадачное Лассо (Multi-Task Lasso)

Мультизадачное Лассо — это линейная модель, которая оценивает редкие коэффициенты для множественных проблем регрессии совместно: Y представляет собой 2D-массив, формы (N_SAMPLES, N_TASKS). Ограничение заключается в том, что выбранные функции одинаковы для всех проблем регрессии, также называемых задачами.

На следующем рисунке сравнивается расположение ненулевых записей в матрице коэффициента W, полученной с помощью простого лассо или многозадачно. Оценки Lasso выросли разбросанные нерешины, в то время как нестерос мультитаскиLasso являются полными столбцами.

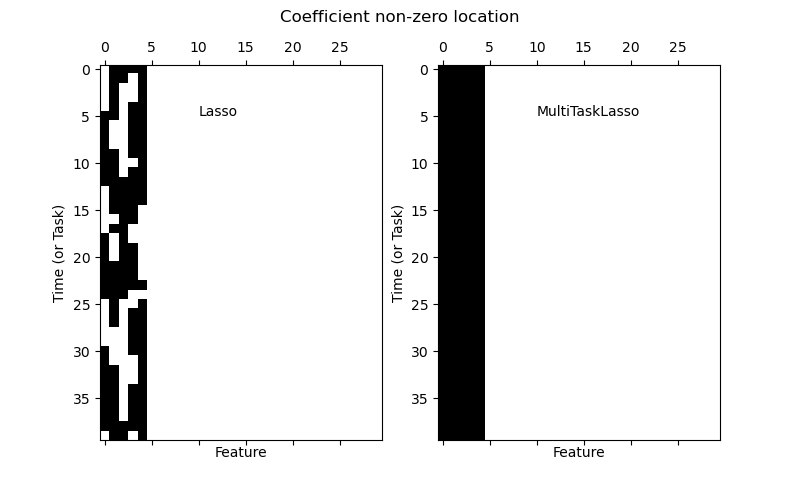
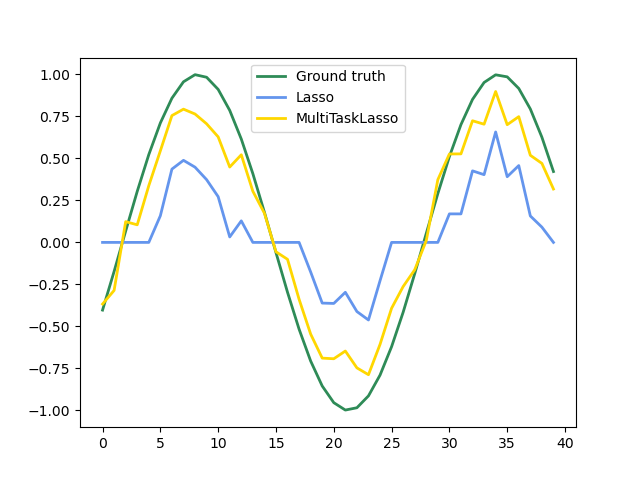
Установка модели серии Time, навязывая, что любая активная функция будет активна в любое время.

Математически он состоит из линейной модели, обученной со смешанным $\ell_1$ $\ell_2$-норма регуляризации. Целевая функция, которую необходимо минимизировать: $$\min_{W} \frac{1}{2n_{\text{samples}}} ||X W — Y||_{\text{Fro}}^2 + \alpha||W||_{21}$$

где $\text{Fro}$ указывает норму Фробениуса $$||A||_{\text{Fro}} = \sqrt{\sum_{ij} a_{ij}^2}$$

а также $\ell_1$ $\ell_2$ читает $$||A||_{2 1} = \sum_i \sqrt{\sum_j a_{ij}^2}$$

Реализация в классе MultiTaskLasso использует спуск координат в качестве алгоритма подбора коэффициентов.

1.1.5. Эластичная сетка

ElasticNet модель линейной регрессии, обученная как $\ell_1$ а также $\ell_2$-нормированная регуляризация коэффициентов. Эта комбинация позволяет изучать разреженную модель, в которой несколько весов не равны нулю Lasso, при сохранении свойств регуляризации Ridge. Контролируем выпуклую комбинацию $\ell_1$ а также $\ell_2$ используя l1_ratio параметр.

Эластичная сетка полезна, когда есть несколько функций, которые коррелируют друг с другом. Лассо, вероятно, выберет одно из них наугад, а эластичная сетка — и то, и другое.

Практическое преимущество компромисса между Lasso и Ridge заключается в том, что он позволяет Elastic-Net унаследовать часть стабильности Ridge при вращении.

Целевая функция для минимизации в этом случае $$\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w — y||_2 ^ 2 + \alpha \rho ||w||_1 + \frac{\alpha(1-\rho)}{2} ||w||_2 ^ 2}$$

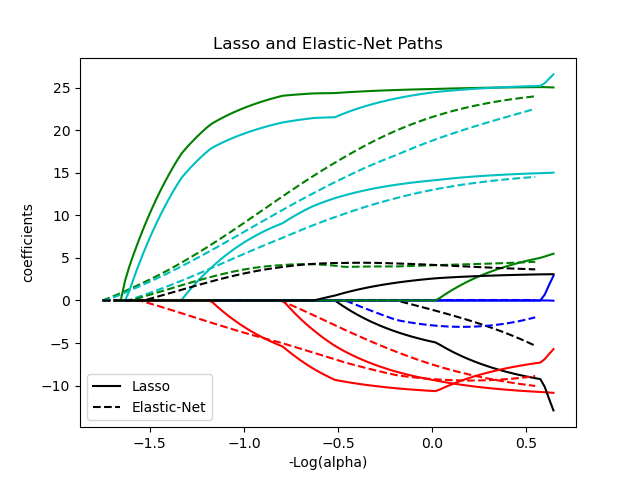
Класс ElasticNetCV можно использовать для установки параметров alpha($\alpha$) и l1_ratio($\rho$) путем перекрестной проверки.

Следующие две ссылки объясняют итерации, используемые в решателе координатного спуска scikit-learn, а также вычисление разрыва двойственности, используемое для управления сходимостью.

1.1.6. Многозадачная Elastic-Net

Это MultiTaskElasticNet модель с эластичной сеткой, которая оценивает разреженные коэффициенты для нескольких задач регрессии совместно: Y представляет собой двумерный массив формы . Ограничение заключается в том, что выбранные функции одинаковы для всех задач регрессии, также называемых задачами. (n_samples, n_tasks)

Математически он состоит из линейной модели, обученной со смешанным $\ell_1$ $\ell_2$-норма и $\ell_2$-норма регуляризации. Целевая функция, которую необходимо минимизировать: $$\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W — Y||_{\text{Fro}}^2 + \alpha \rho ||W||_{2 1} + \frac{\alpha(1-\rho)}{2} ||W||_{\text{Fro}}^2}$$

Реализация в классе MultiTaskElasticNet использует спуск координат в качестве алгоритма подбора коэффициентов.

Класс MultiTaskElasticNetCV можно использовать для установки параметров alpha($\alpha$) и l1_ratio($\rho$) путем перекрестной проверки.

1.1.7. Регрессия наименьшего угла

Регрессия наименьшего угла (LARS) — это алгоритм регрессии для многомерных данных, разработанный Брэдли Эфроном, Тревором Хасти, Иэном Джонстоном и Робертом Тибширани. LARS похож на пошаговую регрессию вперед. На каждом этапе он находит функцию, наиболее коррелирующую с целью. Когда есть несколько объектов, имеющих одинаковую корреляцию, вместо того, чтобы продолжать движение по одному и тому же объекту, он движется в одинаковом направлении между объектами.

Преимущества LARS:

• Он численно эффективен в контекстах, где количество функций значительно превышает количество образцов.
• В вычислительном отношении он так же быстр, как и прямой выбор, и имеет тот же порядок сложности, что и обычный метод наименьших квадратов.
• Он создает полный кусочно-линейный путь решения, который полезен при перекрестной проверке или аналогичных попытках настройки модели.
• Если две характеристики почти одинаково коррелируют с целью, то их коэффициенты должны увеличиваться примерно с одинаковой скоростью. Таким образом, алгоритм ведет себя так, как того и ожидает интуиция, а также является более стабильным.
• Его легко изменить, чтобы получить решения для других оценщиков, таких как Лассо.

К недостаткам метода LARS можно отнести:

• Поскольку LARS основан на итеративном переоснащении остатков, он может оказаться особенно чувствительным к воздействию шума. Эта проблема подробно обсуждается Вайсбергом в разделе обсуждения Efron et al. (2004) Статья Annals of Statistics.

Модель LARS может использоваться с использованием оценки Larsили ее низкоуровневой реализации lars_path или lars_path_gram.

1.1.8. ЛАРС Лассо

LassoLars представляет собой модель лассо, реализованную с использованием алгоритма LARS, и в отличие от реализации, основанной на координатном спуске, это дает точное решение, которое является кусочно-линейным как функция нормы его коэффициентов.

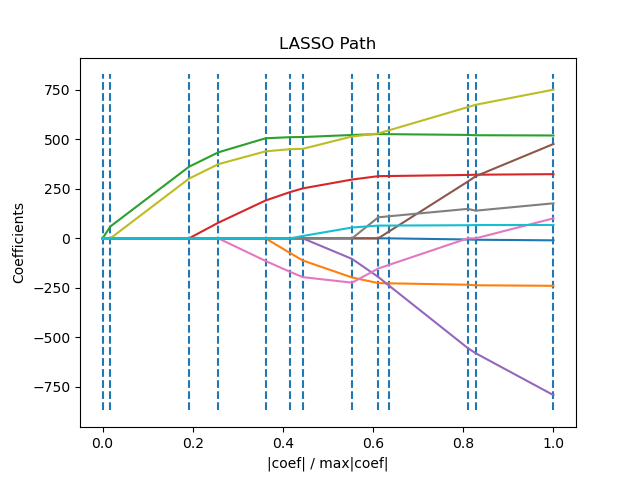
>>> from sklearn import linear_model
>>> reg = linear_model.LassoLars(alpha=.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
LassoLars(alpha=0.1)
>>> reg.coef_
array([0.717157..., 0.        ])

Алгоритм Ларса предоставляет полный путь коэффициентов по параметру регуляризации почти бесплатно, поэтому обычной операцией является получение пути с помощью одной из функций lars_pathили lars_path_gram.

1.1.8.1. Математическая постановка

Алгоритм аналогичен пошаговой регрессии вперед, но вместо того, чтобы включать признаки на каждом шаге, оценочные коэффициенты увеличиваются в направлении, равносильном корреляциям каждого из них с остатком.

Вместо того, чтобы давать векторный результат, решение LARS состоит из кривой, обозначающей решение для каждого значения $\ell_1$ норма вектора параметров. Полный путь коэффициентов хранится в массиве coef_path_, который имеет размер (n_features, max_features + 1). Первый столбец всегда равен нулю.

1.1.9. Ортогональное соответствие (OMP)

OrthogonalMatchingPursuit и orthogonal_mp реализует алгоритм OMP для аппроксимации соответствия линейной модели с ограничениями, наложенными на количество ненулевых коэффициентов (т. е.ℓ0 псевдонорма).

Будучи методом прямого выбора признаков, таким как регрессия по наименьшему углу , поиск ортогонального соответствия может аппроксимировать вектор оптимального решения с фиксированным числом ненулевых элементов: $$\underset{w}{\operatorname{arg\,min\,}} ||y — Xw||_2^2 \text{ subject to } ||w||_0 \leq n_{\text{nonzero_coefs}}$$

В качестве альтернативы, поиск ортогонального сопоставления может нацеливаться на конкретную ошибку вместо определенного количества ненулевых коэффициентов. Это можно выразить как: $$\underset{w}{\operatorname{arg\,min\,}} ||w||_0 \text{ subject to } ||y-Xw||_2^2 \leq \text{tol}$$

1.1.10. Байесовская регрессия

Для включения параметров регуляризации в процедуру оценки можно использовать методы байесовской регрессии: параметр регуляризации не устанавливается в жестком смысле, а настраивается на имеющиеся данные.

Это можно сделать, введя неинформативные априоры над гиперпараметрами модели. В $\ell_{2}$ регуляризация, используемая в регрессии и классификации Риджа, эквивалентна нахождению максимальной апостериорной оценки при гауссовой априорной оценке коэффициентовw с точностью $\lambda^{-1}$. Вместо настройки lambda вручную ее можно рассматривать как случайную величину, которую нужно оценить на основе данных.

Чтобы получить полностью вероятностную модель, на выходе y предполагается, что гауссово распределено вокруг $X w$: $$p(y|X,w,\alpha) = \mathcal{N}(y|X w,\alpha)$$

где α снова рассматривается как случайная величина, которая должна быть оценена на основе данных.

Преимущества байесовской регрессии:

• Он адаптируется к имеющимся данным.
• Его можно использовать для включения параметров регуляризации в процедуру оценки.

К недостаткам байесовской регрессии можно отнести:

• Вывод модели может занять много времени.

1.1.10.1. Регрессия Байесовского хребта

BayesianRidgeоценивает вероятностную модель проблемы регрессии, как описано выше. Приор для коэффициента $w$ дается сферическим гауссианом: $$p(w|\lambda) = \mathcal{N}(w|0,\lambda^{-1}\mathbf{I}_{p})$$

Приоры закончились $\alpha$ а также $\lambda$ выбраны как гамма-распределения , сопряженные априорные для точности гауссианы. Полученная модель называется регрессией Байесовского хребта и аналогична классической Ridge.

Параметры $w$, $\alpha$  а также $\lambda$ оцениваются совместно во время аппроксимации модели, параметры регуляризации $\alpha$ а также $\lambda$ оценивается путем максимизации предельного логарифмического правдоподобия . Реализация scikit-learn основана на алгоритме, описанном в Приложении A (Tipping, 2001), где обновление параметров $\alpha$ а также $\lambda$ делается, как предложено в (MacKay, 1992). Начальное значение процедуры максимизации может быть установлено гиперпараметрами alpha_initи lambda_init.

Есть еще четыре гиперпараметра, $\alpha_1$, $\alpha_2$, $\lambda_1$ а также $\lambda_2$ гамма-априорных распределений по $\alpha$ а также $\lambda$. Обычно они выбираются как неинформативные . По умолчанию $\alpha_1 = \alpha_2 = \lambda_1 = \lambda_2 = 10^{-6}$.

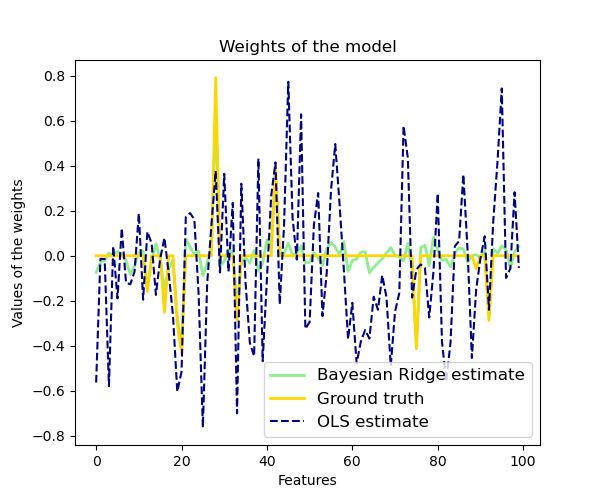
Регрессия Байесовского хребта используется для регрессии:

>>> from sklearn import linear_model
>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]
>>> Y = [0., 1., 2., 3.]
>>> reg = linear_model.BayesianRidge()
>>> reg.fit(X, Y)
BayesianRidge()

После установки модель может быть использована для прогнозирования новых значений:

>>> reg.predict([[1, 0.]])
array([0.50000013])

Коэффициенты w модели доступны:

>>> reg.coef_
array([0.49999993, 0.49999993])

Из-за байесовской структуры найденные веса немного отличаются от весов, найденных с помощью обыкновенных наименьших квадратов . Однако регрессия Байесовского хребта более устойчива к некорректно поставленным задачам.

1.1.10.2. Автоматическое определение релевантности — ARD

ARDRegression очень похожа на регрессию Байесовского хребта , но может приводить к более разреженным коэффициентам $w$ (рекомендации 1 и 2). ARDRegressionставит другой приоритет передw, отказавшись от предположения, что гауссиан является сферическим.

Вместо этого распределение по w считается параллельным осям эллиптическим распределением Гаусса.

Это означает, что каждый коэффициент wi берется из распределения Гаусса с центром в нуле и с точностью λi: $$p(w|\lambda) = \mathcal{N}(w|0,A^{-1})$$

с участием $\text{diag}(A) = \lambda = {\lambda_{1},…,\lambda_{p}}$.

В отличие от регрессии Байесовского хребта , каждая координатаwi имеет собственное стандартное отклонение $\lambda_i$. Приоритет во всемλi выбрано такое же гамма-распределение, заданное гиперпараметрами $\lambda_1$ а также $\lambda_2$.

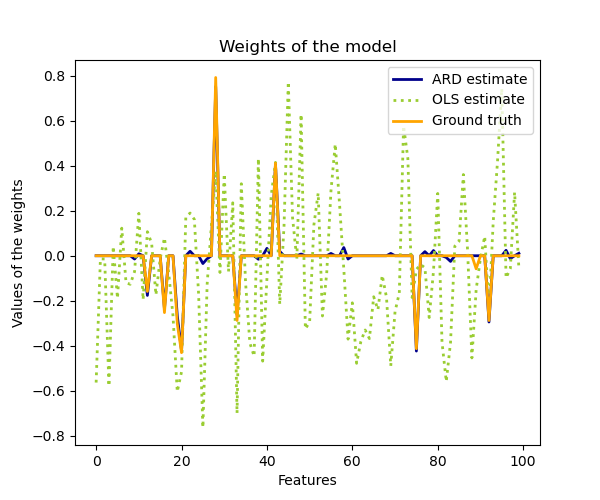
ARD также известен в литературе как машина разреженного байесовского обучения и векторов релевантности (рекомендации 3 и 4).

1.1.11. Логистическая регрессия

Логистическая регрессия, несмотря на свое название, представляет собой скорее линейную модель классификации, чем регрессию. Логистическая регрессия также известна в литературе как логит-регрессия, классификация максимальной энтропии (MaxEnt) или лог-линейный классификатор. В этой модели вероятности, описывающие возможные результаты одного испытания, моделируются с использованием логистической функции.

Логистическая регрессия реализована в LogisticRegression. Эта реализация может соответствовать бинарной, однозначной или полиномиальной логистической регрессии с необязательной $\ell_1$, $\ell_2$ или регуляризация Elastic-Net.

В качестве проблемы оптимизации двоичный класс $\ell_2$ штрафная логистическая регрессия минимизирует следующую функцию затрат: $$\min_{w, c} \frac{1}{2}w^T w + C \sum_{i=1}^n \log(\exp(- y_i (X_i^T w + c)) + 1) .$$

По аналогии, $\ell_1$ регуляризованная логистическая регрессия решает следующую задачу оптимизации: $$\min_{w, c} |w|_1 + C \sum_{i=1}^n \log(\exp(- y_i (X_i^T w + c)) + 1).$$

Регуляризация Elastic-Net представляет собой комбинацию $\ell_1$ а также $\ell_2$, и минимизирует следующую функцию стоимости:$$\min_{w, c} \frac{1 — \rho}{2}w^T w + \rho |w|_1 + C \sum_{i=1}^n \log(\exp(- y_i (X_i^T w + c)) + 1),$$

где $\rho$ контролирует силу $\ell_1$ регуляризация против $\ell_2$ регуляризация (соответствует l1_ratio параметру).

Обратите внимание, что в этих обозначениях предполагается, что цель $y_i$ принимает значения в наборе ${-1, 1}$ по $i$. Мы также можем видеть, что Elastic-Net эквивалентен $\ell_1$ когда $\rho = 1$ и эквивалент $\ell_2$ когда $\rho = 0$.

В классе реализованы решатели LogisticRegression liblinear, newton-cg, lbfgs, sag и saga:

Решатель liblinear использует алгоритм координатного спуска (КД) и полагается на отличную библиотеку C ++ LIBLINEAR , которая поставляется с scikit-learn. Однако алгоритм КД, реализованный в liblinear, не может изучить истинную полиномиальную (мультиклассовую) модель; вместо этого проблема оптимизации декомпозируется по принципу «один против остальных», поэтому отдельные двоичные классификаторы обучаются для всех классов. Это происходит под капотом, поэтому LogisticRegression экземпляры, использующие этот решатель, ведут себя как мультиклассовые классификаторы. Для $\ell_1$ регуляризация sklearn.svm.l1_min_c позволяет вычислить нижнюю границу для C, чтобы получить ненулевую (все веса признаков равны нулю) модель.

Решатели «lbfgs», «sag» и «newton-cg» поддерживают только $\ell_2$ регуляризация или отсутствие регуляризации, и обнаружено, что они сходятся быстрее для некоторых многомерных данных. Установка multi_class «полиномиального» с помощью этих решателей позволяет изучить истинную полиномиальную модель логистической регрессии (источник 5), что означает, что ее оценки вероятности должны быть лучше откалиброваны, чем настройка «один против остальных» по умолчанию.

Решатель «sag» использует спуск градиента стохастического среднего (источник 6). Это быстрее, чем другие решатели для больших наборов данных, когда и количество выборок, и количество объектов велико.

Решатель «saga» (источник 7) представляет собой вариант «провисания», который также поддерживает негладкие penalty="l1". Таким образом, это предпочтительный решатель для разреженной полиномиальной логистической регрессии. Это также единственный решатель, который поддерживает penalty="elasticnet".

«Lbfgs» — это алгоритм оптимизации, который приближает алгоритм Бройдена – Флетчера – Гольдфарба – Шанно (источник 8) , который принадлежит к квазиньютоновским методам. Решатель «lbfgs» рекомендуется использовать для небольших наборов данных, но для больших наборов данных страдает его производительность. (источник 9)

В следующей таблице приведены штрафы, поддерживаемые каждым решателем:

Решатель «lbfgs» используется по умолчанию из-за его надежности. Для больших наборов данных решатель «saga» обычно работает быстрее. Для большого набора данных вы также можете рассмотреть возможность использования SGDClassifierс потерей журнала, что может быть даже быстрее, но требует дополнительной настройки.

LogisticRegressionCV реализует логистическую регрессию со встроенной поддержкой перекрестной проверки, чтобы найти оптимальные параметры C и l1_ratio параметры в соответствии с scoring атрибутом. Решатели «newton-cg», «sag», «saga» и «lbfgs» оказались более быстрыми для данных с высокой плотностью измерений из-за горячего старта (см. Глоссарий ).

1.1.12. Обобщенная линейная регрессия

Обобщенные линейные модели (GLM) расширяют линейные модели двумя способами (Источник 10). Во-первых, прогнозируемые значения $\hat{y}$ связаны с линейной комбинацией входных переменных $X$ через функцию обратной связи $h$ в виде $$\hat{y}(w, X) = h(Xw).$$

Во-вторых, функция потерь в квадрате заменяется единичным отклонением $d$ распределения в экспоненциальном семействе (или, точнее, репродуктивной модели экспоненциальной дисперсии (EDM) (Источник 11) ).

Проблема минимизации становится: $$\min_{w} \frac{1}{2 n_{\text{samples}}} \sum_i d(y_i, \hat{y}_i) + \frac{\alpha}{2} ||w||_2,$$

где $\alpha$ штраф регуляризации L2. Если указаны веса выборки, среднее значение становится средневзвешенным.

В следующей таблице перечислены некоторые конкретные EDM и их единичное отклонение (все они являются экземплярами семейства Tweedie):

Функции Плотности Вероятности (ФПВ) этих распределений показаны на следующем рисунке.

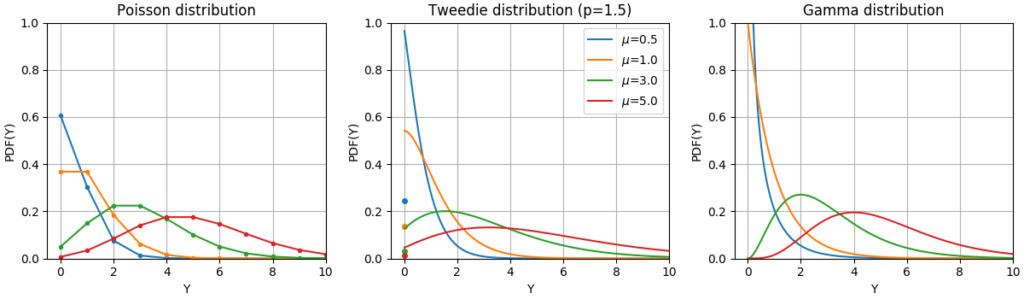
ФПВ случайной величины Y после распределений Пуассона, Твиди (мощность = 1,5) и гамма-распределения с разными средними значениями ($\mu$). Обратите внимание на точечную массу на $Y=0$ для распределения Пуассона и распределения Твиди (power = 1,5), но не для гамма-распределения, которое имеет строго положительный целевой домен. 

Выбор распределения зависит от решаемой задачи:

• Если целевые значения $y$ являются счетчиками (неотрицательные целые числа) или относительными частотами (неотрицательными), вы можете использовать отклонение Пуассона с лог-связью.
• Если целевые значения положительны и искажены, вы можете попробовать гамма-отклонение с лог-ссылкой.
• Если целевые значения кажутся более тяжелыми, чем у гамма-распределения, вы можете попробовать обратное гауссовское отклонение (или даже более высокие степени дисперсии семейства Твиди).

Примеры вариантов использования включают:

• Моделирование сельского хозяйства / погоды: количество дождевых явлений в год (Пуассон), количество осадков на одно событие (Гамма), общее количество осадков в год (Твиди / Составная Пуассоновская гамма).
• Моделирование рисков / ценообразование страховых полисов: количество событий по претензиям / держателя полиса в год (Пуассон), стоимость за событие (гамма), общие затраты на держателя полиса в год (твиди / сложная гамма Пуассона).
• Профилактическое обслуживание: количество событий прерывания производства в год (Пуассон), продолжительность прерывания (Гамма), общее время прерывания в год (Твиди / Составная гамма Пуассона).

1.1.12.1. Использование

TweedieRegressor реализует обобщенную линейную модель для распределения Твиди, которая позволяет моделировать любое из вышеупомянутых распределений с использованием соответствующего power параметра. В частности:

• power = 0: Нормальное распределение. В этом случае Ridge, ElasticNet как правило, более уместны специальные оценки, такие как.
• power = 1: Распределение Пуассона. PoissonRegressor выставлен для удобства. Однако это строго эквивалентно .TweedieRegressor(power=1, link='log')
• power = 2: Гамма-распределение. GammaRegressor выставлен для удобства. Однако это строго эквивалентно TweedieRegressor(power=2, link='log')
• power = 3: Обратное распределение Гаусса.

Функция связи определяется link параметром.

Пример использования:

>>> from sklearn.linear_model import TweedieRegressor
>>> reg = TweedieRegressor(power=1, alpha=0.5, link='log')
>>> reg.fit([[0, 0], [0, 1], [2, 2]], [0, 1, 2])
TweedieRegressor(alpha=0.5, link='log', power=1)
>>> reg.coef_
array([0.2463..., 0.4337...])
>>> reg.intercept_
-0.7638...

1.1.12.2. Практические соображения

Перед подгонкой матрица характеристик $X$ должна быть стандартизирована. Это гарантирует, что штраф учитывает особенности одинаково.

Поскольку линейный предиктор $Xw$ может быть отрицательным, а распределения Пуассона, Гамма и Обратный Гаусс не поддерживают отрицательные значения, необходимо применить функцию обратной связи, которая гарантирует неотрицательность. Например link='log', функция обратной связи становится $h(Xw)=\exp(Xw)$.

Если вы хотите смоделировать относительную частоту, то есть количество импульсов на экспозицию (время, объем,…), вы можете сделать это, используя распределение Пуассона и передавая $y=\frac{\mathrm{counts}}{\mathrm{exposure}}$ в качестве целевых значений вместе с $\mathrm{exposure}$ качестве гирь для образцов. Конкретный пример см., Например, в регрессии Твиди по страховым случаям .

При выполнении перекрестной проверки для power параметра TweedieRegressor желательно указать явную scoring функцию, поскольку счетчик по умолчанию TweedieRegressor.score является функцией самого power себя.

1.1.13. Стохастический градиентный спуск — SGD

Стохастический градиентный спуск — это простой, но очень эффективный подход для подбора линейных моделей. Это особенно полезно, когда количество образцов (и количество функций) очень велико. partial_fit Метод позволяет онлайн / вне основного обучения.

Классы SGDClassifier и SGDRegressor предоставляют функциональные возможности для соответствия линейным моделям классификации и регрессии с использованием различных (выпуклых) функций потерь и различных штрафов. Например, с loss="log", SGDClassifier подходит для модели логистической регрессии, а с loss="hinge" ним подходит для линейной машины опорных векторов (SVM).

1.1.14. Персептрон

Это Perceptron еще один простой алгоритм классификации, подходящий для крупномасштабного обучения. По умолчанию:

• Не требует скорости обучения
• Это не регуляризовано (наказано).
• Обновляет свою модель только на ошибках.

Последняя характеристика подразумевает, что Perceptron обучается немного быстрее, чем SGD, с потерей шарниров, и что получаемые модели реже.

1.1.15. Пассивные агрессивные алгоритмы

Пассивно-агрессивные алгоритмы — это семейство алгоритмов для крупномасштабного обучения. Они похожи на перцептрон в том, что не требуют скорости обучения. Однако, в отличие от перцептрона, они включают параметр регуляризации C.

Для классификации PassiveAggressiveClassifier может использоваться с loss='hinge'(PA-I) или loss='squared_hinge' (PA-II). Для регрессии PassiveAggressiveRegressor можно использовать loss='epsilon_insensitive'(PA-I) или loss='squared_epsilon_insensitive'(PA-II).

1.1.16. Регрессия устойчивости: выбросы и ошибки моделирования

Устойчивая регрессия направлена ​​на то, чтобы соответствовать модели регрессии при наличии искаженных данных: либо выбросов, либо ошибки в модели.

1.1.16.1. Разные сценарии и полезные концепции

При работе с данными, поврежденными выбросами, следует помнить следующее:

• Выбросы в X или Y ?

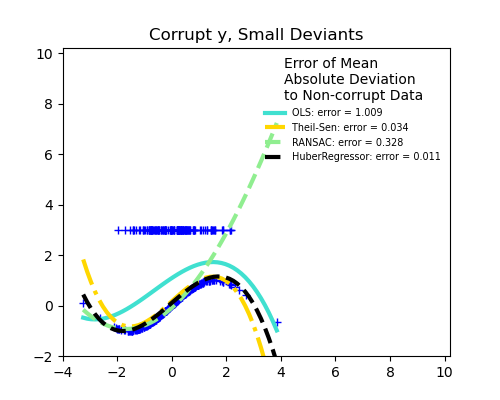
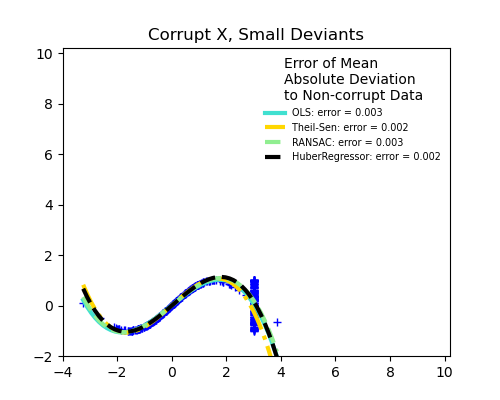
• Доля выбросов в зависимости от амплитуды ошибки

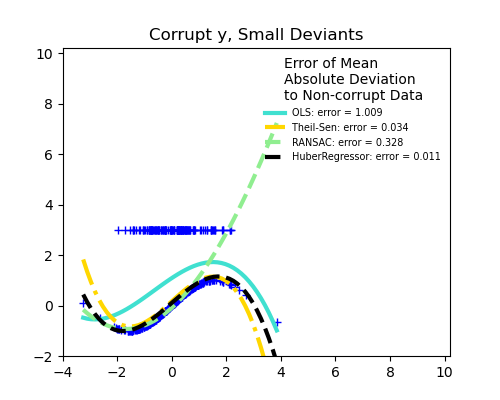
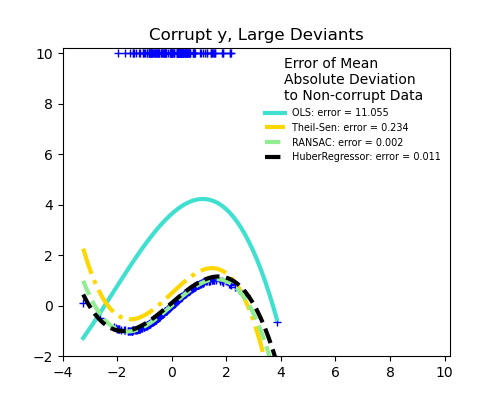
Важным понятием надежной подгонки является понятие точки разбиения: часть данных, которая может оказаться за пределами подгонки, чтобы начать пропускать входящие данные.

Обратите внимание, что в целом надежная установка в условиях большого размера (большого размера n_features) очень сложна. Приведенные здесь надежные модели, вероятно, не будут работать в этих условиях.

1.1.16.2. RANSAC: СЛУЧАЙНЫЙ ШИРОКИЙ КОНСенсус

RANSAC (RANdom SAmple Consensus) соответствует модели из случайных подмножеств вставок из полного набора данных.

RANSAC — это недетерминированный алгоритм, дающий только разумный результат с определенной вероятностью, которая зависит от количества итераций (см. max_trials параметр). Он обычно используется для задач линейной и нелинейной регрессии и особенно популярен в области фотограмметрического компьютерного зрения.

Алгоритм разбивает полные входные данные выборки на набор выбросов, которые могут быть подвержены шуму, и выбросов, которые, например, вызваны ошибочными измерениями или неверными гипотезами о данных. Результирующая модель затем оценивается только по определенным меткам.

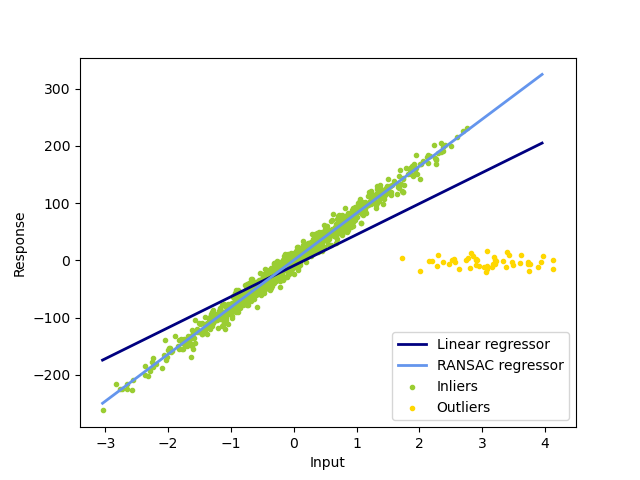
1.1.16.2.1. Детали алгоритма

Каждая итерация выполняет следующие шаги:

1. Выберите min_samples случайные выборки из исходных данных и проверьте, верен ли набор данных (см. is_data_valid).
2. Подгоните модель к случайному подмножеству ( base_estimator.fit) и проверьте, действительна ли оценочная модель (см. is_model_valid).
3. Классифицируйте все данные как выбросы или выбросы, вычислив остатки по оценочной модели (base_estimator.predict(X) — y) — все выборки данных с абсолютными остатками меньше, чем отклонения, рассматриваются как выбросы. residual_threshold
4. Сохраните подобранную модель как лучшую модель, если количество вставок максимально. В случае, если текущая оценочная модель имеет такое же количество вставок, она считается лучшей только в том случае, если у нее лучший результат.

Эти шаги выполняются либо максимальное количество раз ( max_trials), либо до тех пор, пока не будет выполнен один из специальных критериев остановки (см. stop_n_inliers и stop_score). Окончательная модель оценивается с использованием всех промежуточных выборок (консенсусного набора) ранее определенной лучшей модели.

Функции is_data_valid и is_model_valid позволяют идентифицировать и отклонять вырожденные комбинации случайных подвыборок. Если оценочная модель не требуется для выявления вырожденных случаев, is_data_valid ее следует использовать в том виде, в котором она вызывается до подгонки модели, что, таким образом, приведет к повышению производительности вычислений.

1.1.16.3. Оценка Тейла-Сена: оценка на основе обобщенной медианы

TheilSenRegressor оценки использует обобщение медианы в нескольких измерениях. Таким образом, он устойчив к многомерным выбросам. Однако обратите внимание, что надежность оценки быстро снижается с увеличением размерности проблемы. Он теряет свои свойства устойчивости и становится не лучше, чем обычный метод наименьших квадратов в большой размерности.

1.1.16.3.1. Теоретические соображения

TheilSenRegressor сравнимо с методом наименьших квадратов (OLS) с точки зрения асимптотической эффективности и несмещенной оценки. В отличие от OLS, Theil-Sen — это непараметрический метод, что означает, что он не делает никаких предположений о базовом распределении данных. Поскольку Theil-Sen — это средство оценки на основе медианы, оно более устойчиво к искаженным данным, также известным как выбросы. В одномерном параметре Theil-Sen имеет точку разбивки около 29,3% в случае простой линейной регрессии, что означает, что он может допускать произвольные искаженные данные до 29,3%.

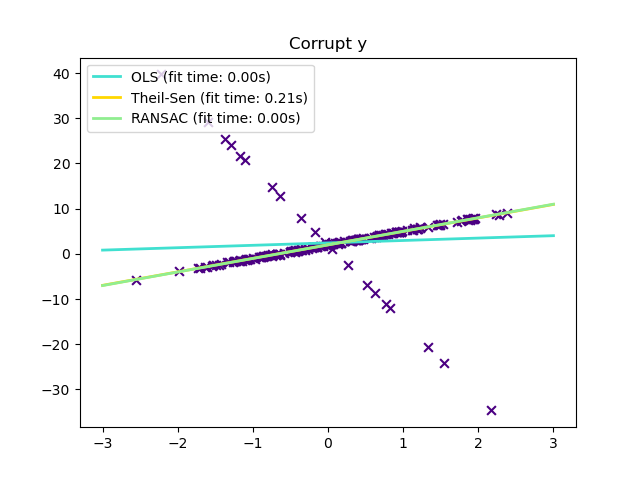
Реализация TheilSenRegressor in scikit-learn следует за обобщением модели многомерной линейной регрессии (источник 12) с использованием пространственной медианы, которая является обобщением медианы на несколько измерений (источник 13).

С точки зрения временной и пространственной сложности, Theil-Sen масштабируется в соответствии с $$\binom{n_{\text{samples}}}{n_{\text{subsamples}}}$$

что делает невозможным его исчерпывающее применение к проблемам с большим количеством образцов и функций. Следовательно, можно выбрать размер субпопуляции, чтобы ограничить временную и пространственную сложность, рассматривая только случайное подмножество всех возможных комбинаций.

1.1.16.4. Регрессия Хубера

Это HuberRegressor отличается от того, Ridge что он применяет линейные потери к выборкам, которые классифицируются как выбросы. Выборка классифицируется как промежуточная, если абсолютная ошибка этой выборки меньше определенного порога. Он отличается от TheilSenRegressorи RANSACRegressor тем, что не игнорирует влияние выбросов, но придает им меньший вес.

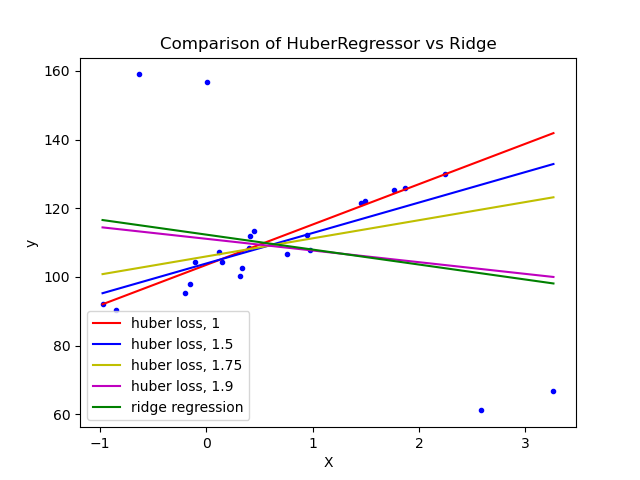
Функция потерь, которая HuberRegressor минимизирует, определяется выражением $$\min_{w, \sigma} {\sum_{i=1}^n\left(\sigma + H_{\epsilon}\left(\frac{X_{i}w — y_{i}}{\sigma}\right)\sigma\right) + \alpha {||w||_2}^2}$$

где $$\begin{split}H_{\epsilon}(z) = \begin{cases} z^2, & \text {if } |z| < \epsilon, \ 2\epsilon|z| — \epsilon^2, & \text{otherwise} \end{cases}\end{split}$$

Рекомендуется установить параметр epsilon на 1,35 для достижения статистической эффективности 95%.

1.1.16.5. Примечания

В HuberRegressor отличается от использования SGDRegressor с набором потерь для huberследующим образом.

• HuberRegressorмасштабирующий инвариант. После epsilon установки масштабирование  X и y уменьшение или увеличение на разные значения обеспечит такую ​​же устойчивость к выбросам, как и раньше. по сравнению с SGDRegressor которой epsilon должен быть установлен снова , когда X и y масштабируются.
• HuberRegressor должен быть более эффективным для использования с данными с небольшим количеством выборок, в то время как SGDRegressor для получения такой же надежности требуется несколько проходов обучающих данных.

Обратите внимание, что эта оценка отличается от реализации Робастной регрессии ( http://www.ats.ucla.edu/stat/r/dae/rreg.htm ), поскольку реализация R выполняет взвешенную реализацию методом наименьших квадратов с весами, присвоенными каждую выборку на основании того, насколько остаток превышает определенный порог.

1.1.17. Полиномиальная регрессия: расширение линейных моделей с помощью базисных функций

Один из распространенных паттернов машинного обучения — использование линейных моделей, обученных нелинейным функциям данных. Такой подход обеспечивает в целом высокую производительность линейных методов, позволяя им приспосабливать гораздо более широкий диапазон данных.

Например, простая линейная регрессия может быть расширена путем построения полиномиальных функций из коэффициентов. В случае стандартной линейной регрессии у вас может быть модель, которая выглядит следующим образом для двумерных данных: $$\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2$$

Если мы хотим подогнать к данным параболоид, а не плоскость, мы можем объединить функции в полиномы второго порядка, чтобы модель выглядела так: $$\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2 + w_3 x_1 x_2 + w_4 x_1^2 + w_5 x_2^2$$

Наблюдение (иногда удивительное) заключается в том, что это все еще линейная модель : чтобы убедиться в этом, представьте, что вы создаете новый набор функций. $$z = [x_1, x_2, x_1 x_2, x_1^2, x_2^2]$$

С этой перемаркировкой данных наша проблема может быть записана $$\hat{y}(w, z) = w_0 + w_1 z_1 + w_2 z_2 + w_3 z_3 + w_4 z_4 + w_5 z_5$$

Мы видим, что полученная полиномиальная регрессия относится к тому же классу линейных моделей, который мы рассмотрели выше (т.е. модель линейна поw) и могут быть решены теми же методами. Рассматривая линейные соответствия в многомерном пространстве, построенном с помощью этих базовых функций, модель обладает гибкостью, позволяющей соответствовать гораздо более широкому диапазону данных.

Вот пример применения этой идеи к одномерным данным с использованием полиномиальных функций разной степени:

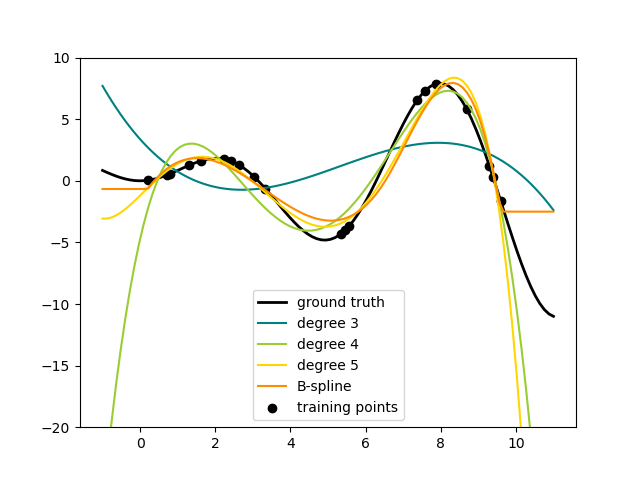
Этот рисунок создается с помощью PolynomialFeatures преобразователя, который преобразует матрицу входных данных в новую матрицу данных заданной степени. Его можно использовать следующим образом:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

Особенности $X$ были преобразованы из $[x_1, x_2]$ к $[1, x_1, x_2, x_1^2, x_1 x_2, x_2^2]$, и теперь может использоваться в любой линейной модели.

Такого рода предварительную обработку можно упростить с помощью инструментов конвейера. Один объект, представляющий простую полиномиальную регрессию, может быть создан и использован следующим образом:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
...                   ('linear', LinearRegression(fit_intercept=False))])
>>> # fit to an order-3 polynomial data
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2.,  1., -1.])

Линейная модель, обученная полиномиальным признакам, способна точно восстановить входные коэффициенты полинома.

В некоторых случаях необязательно включать более высокую степень какой-либо отдельной функции, а только так называемые функции взаимодействия, которые не более чем умножаются друг на друга $d$ отличительные особенности. Их можно получить PolynomialFeaturesс помощью настройки interaction_only=True.

Например, при работе с логическими функциями $x_i^n = x_i$ для всех nи поэтому бесполезен; но $x_i x_j$ представляет собой соединение двух логических значений. Таким образом, мы можем решить проблему XOR с помощью линейного классификатора:

>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
       [1, 0, 1, 0],
       [1, 1, 0, 0],
       [1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, max_iter=10, tol=None,
...                  shuffle=False).fit(X, y)

И «предсказания» классификатора идеальны:

>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0