1.10. Деревья решений ¶
Деревья решений (DT) — это непараметрический контролируемый метод обучения, используемый для классификации и регрессии . Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной, изучая простые правила принятия решений, выведенные из характеристик данных. Дерево можно рассматривать как кусочно-постоянное приближение.
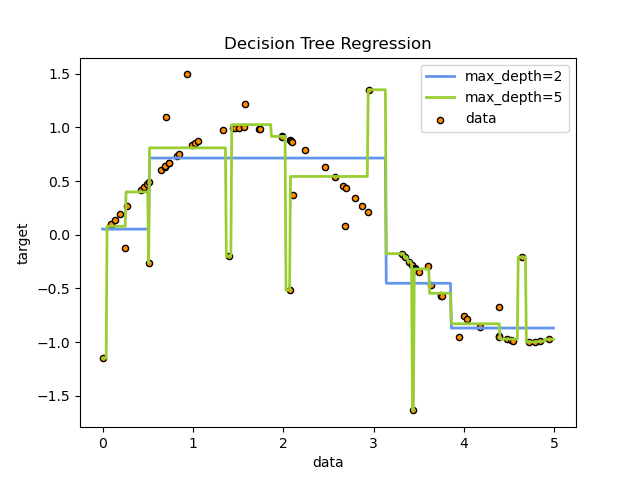
Например, в приведенном ниже примере деревья решений обучаются на основе данных, чтобы аппроксимировать синусоидальную кривую с набором правил принятия решений «если-то-еще». Чем глубже дерево, тем сложнее правила принятия решений и тем лучше модель.
Некоторые преимущества деревьев решений:
- Просто понять и интерпретировать. Деревья можно визуализировать.
- Требуется небольшая подготовка данных. Другие методы часто требуют нормализации данных, создания фиктивных переменных и удаления пустых значений. Однако обратите внимание, что этот модуль не поддерживает отсутствующие значения.
- Стоимость использования дерева (т. Е. Прогнозирования данных) является логарифмической по количеству точек данных, используемых для обучения дерева.
- Может обрабатывать как числовые, так и категориальные данные. Однако реализация scikit-learn пока не поддерживает категориальные переменные. Другие методы обычно специализируются на анализе наборов данных, содержащих только один тип переменных. См. Алгоритмы для получения дополнительной информации.
- Способен обрабатывать проблемы с несколькими выходами.
- Использует модель белого ящика. Если данная ситуация наблюдаема в модели, объяснение условия легко объяснить с помощью булевой логики. Напротив, в модели черного ящика (например, в искусственной нейронной сети) результаты могут быть труднее интерпретировать.
- Возможна проверка модели с помощью статистических тестов. Это позволяет учитывать надежность модели.
- Работает хорошо, даже если его предположения несколько нарушаются истинной моделью, на основе которой были сгенерированы данные.
К недостаткам деревьев решений можно отнести:
- Обучающиеся дереву решений могут создавать слишком сложные деревья, которые плохо обобщают данные. Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка максимальной глубины дерева.
- Деревья решений могут быть нестабильными, поскольку небольшие изменения в данных могут привести к созданию совершенно другого дерева. Эта проблема смягчается за счет использования деревьев решений в ансамбле.
- Как видно из рисунка выше, предсказания деревьев решений не являются ни гладкими, ни непрерывными, а являются кусочно-постоянными приближениями. Следовательно, они не годятся для экстраполяции.
- Известно, что проблема обучения оптимальному дереву решений является NP-полной с точки зрения нескольких аспектов оптимальности и даже для простых концепций. Следовательно, практические алгоритмы обучения дереву решений основаны на эвристических алгоритмах, таких как жадный алгоритм, в котором локально оптимальные решения принимаются в каждом узле. Такие алгоритмы не могут гарантировать возврат глобального оптимального дерева решений. Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой.
- Существуют концепции, которые трудно изучить, поскольку деревья решений не выражают их легко, например проблемы XOR, четности или мультиплексора.
- Ученики дерева решений создают предвзятые деревья, если некоторые классы доминируют. Поэтому рекомендуется сбалансировать набор данных перед подгонкой к дереву решений.
1.10.1. Классификация
DecisionTreeClassifier — это класс, способный выполнять мультиклассовую классификацию набора данных.
Как и в случае с другими классификаторами, DecisionTreeClassifier принимает в качестве входных данных два массива: массив X, разреженный или плотный, формы (n_samples, n_features), содержащий обучающие образцы, и массив Y целочисленных значений, формы (n_samples,), содержащий метки классов для обучающих образцов:
>>> from sklearn import tree >>> X = [[0, 0], [1, 1]] >>> Y = [0, 1] >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, Y)
После подбора модель можно использовать для прогнозирования класса образцов:
>>> clf.predict([[2., 2.]]) array([1])
В случае, если существует несколько классов с одинаковой и самой высокой вероятностью, классификатор предскажет класс с самым низким индексом среди этих классов.
В качестве альтернативы выводу определенного класса можно предсказать вероятность каждого класса, которая представляет собой долю обучающих выборок класса в листе:
>>> clf.predict_proba([[2., 2.]]) array([[0., 1.]])
DecisionTreeClassifier поддерживает как двоичную (где метки — [-1, 1]), так и мультиклассовую (где метки — [0,…, K-1]) классификацию.
Используя набор данных Iris, мы можем построить дерево следующим образом:
>>> from sklearn.datasets import load_iris >>> from sklearn import tree >>> iris = load_iris() >>> X, y = iris.data, iris.target >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, y)
После обучения вы можете построить дерево с помощью plot_tree функции:
>>> tree.plot_tree(clf)
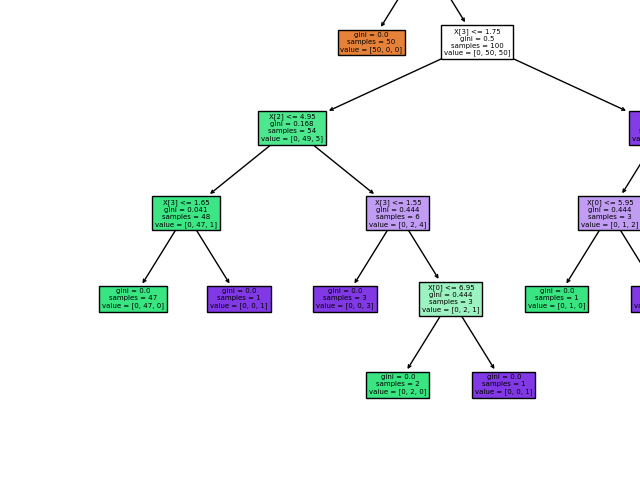
Мы также можем экспортировать дерево в формат Graphviz с помощью export_graphviz экспортера. Если вы используете Conda менеджер пакетов, то Graphviz бинарные файлы и пакет питон может быть установлен conda install python-graphviz.
В качестве альтернативы двоичные файлы для graphviz можно загрузить с домашней страницы проекта graphviz, а оболочку Python установить из pypi с помощью pip install graphviz.
Ниже приведен пример экспорта graphviz вышеуказанного дерева, обученного на всем наборе данных радужной оболочки глаза; результаты сохраняются в выходном файле iris.pdf:
>>> import graphviz
>>> dot_data = tree.export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris") Экспортер export_graphviz также поддерживает множество эстетических вариантов, в том числе окраски узлов их класс (или значение регрессии) и используя явные имена переменных и классов , если это необходимо. Блокноты Jupyter также автоматически отображают эти графики встроенными:
>>> dot_data = tree.export_graphviz(clf, out_file=None, ... feature_names=iris.feature_names, ... class_names=iris.target_names, ... filled=True, rounded=True, ... special_characters=True) >>> graph = graphviz.Source(dot_data) >>> graph
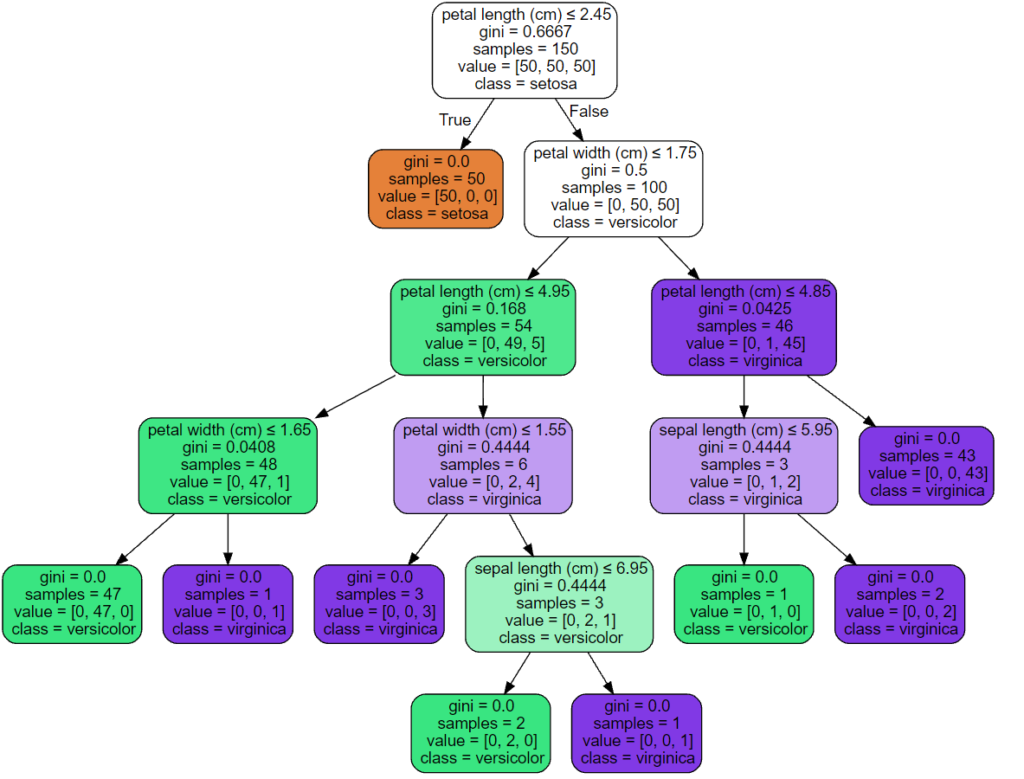
В качестве альтернативы дерево можно также экспортировать в текстовый формат с помощью функции export_text. Этот метод не требует установки внешних библиотек и более компактен:
>>> from sklearn.datasets import load_iris >>> from sklearn.tree import DecisionTreeClassifier >>> from sklearn.tree import export_text >>> iris = load_iris() >>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2) >>> decision_tree = decision_tree.fit(iris.data, iris.target) >>> r = export_text(decision_tree, feature_names=iris['feature_names']) >>> print(r) |--- petal width (cm) <= 0.80 | |--- class: 0 |--- petal width (cm) > 0.80 | |--- petal width (cm) <= 1.75 | | |--- class: 1 | |--- petal width (cm) > 1.75 | | |--- class: 2
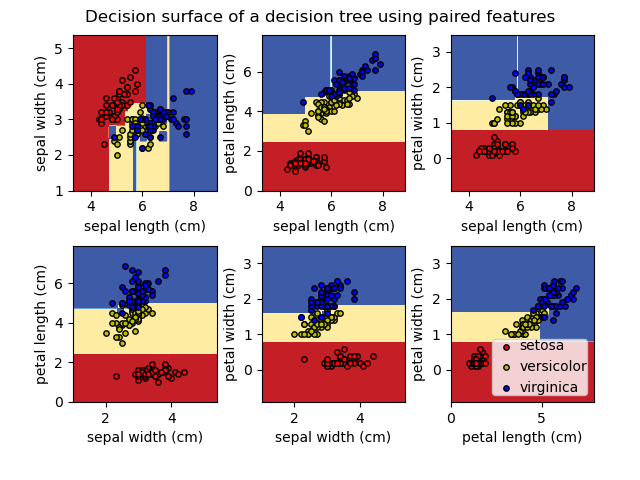
Примеры
1.10.2. Регрессия
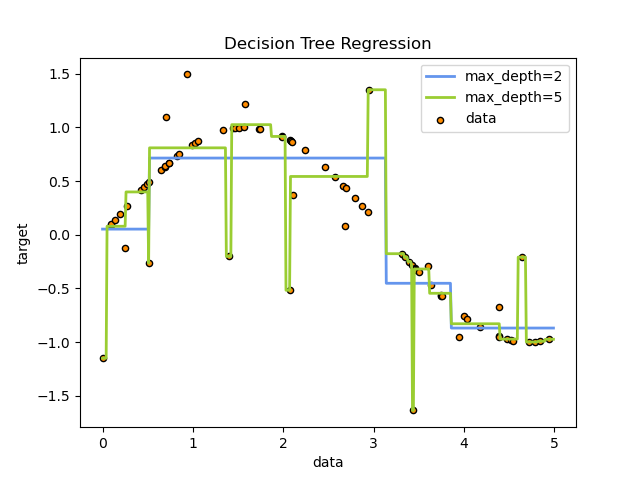
Деревья решений также могут применяться к задачам регрессии с помощью класса DecisionTreeRegressor .
Как и в настройке классификации, метод fit будет принимать в качестве аргументов массивы X и y, только в этом случае ожидается, что y будет иметь значения с плавающей запятой вместо целочисленных значений:
>>> from sklearn import tree >>> X = [[0, 0], [2, 2]] >>> y = [0.5, 2.5] >>> clf = tree.DecisionTreeRegressor() >>> clf = clf.fit(X, y) >>> clf.predict([[1, 1]]) array([0.5])
Пример:
1.10.3. Проблемы с несколькими выходами
Задача с несколькими выходами — это проблема контролируемого обучения с несколькими выходами для прогнозирования, то есть когда Y — это 2-й массив формы (n_samples, n_outputs).
Когда нет корреляции между выходами, очень простой способ решить эту проблему — построить n независимых моделей, то есть по одной для каждого выхода, а затем использовать эти модели для независимого прогнозирования каждого из n выходов. Однако, поскольку вполне вероятно, что выходные значения, относящиеся к одному и тому же входу, сами коррелированы, часто лучшим способом является построение единой модели, способной прогнозировать одновременно все n выходов. Во-первых, это требует меньшего времени на обучение, поскольку строится только один оценщик. Во-вторых, часто можно повысить точность обобщения итоговой оценки.
Что касается деревьев решений, эту стратегию можно легко использовать для поддержки задач с несколькими выходами. Для этого требуются следующие изменения:
- Сохранять n выходных значений в листьях вместо 1;
- Используйте критерии разделения, которые вычисляют среднее сокращение для всех n выходов.
Этот модуль предлагает поддержку для задач с несколькими выходами, реализуя эту стратегию как в, так DecisionTreeClassifier и в DecisionTreeRegressor. Если дерево решений соответствует выходному массиву Y формы (n_samples, n_outputs), то итоговая оценка будет:
- Вывести значения n_output при
predict; - Выведите список массивов n_output вероятностей классов на
predict_proba.
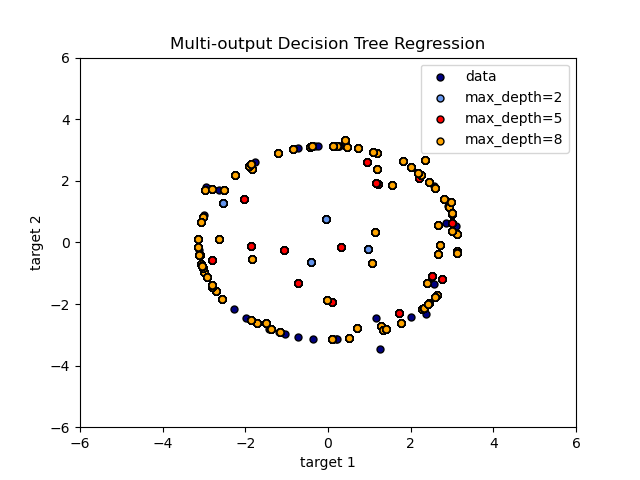
Использование деревьев с несколькими выходами для регрессии продемонстрировано в разделе «Регрессия дерева решений с несколькими выходами» . В этом примере вход X — это одно действительное значение, а выходы Y — синус и косинус X.
Использование деревьев с несколькими выходами для классификации демонстрируется в разделе «Завершение лица с оценками с несколькими выходами» . В этом примере входы X — это пиксели верхней половины граней, а выходы Y — пиксели нижней половины этих граней.

Примеры:
Рекомендации:
- М. Дюмон и др., Быстрая мультиклассовая аннотация изображений со случайными подокнами и множественными выходными рандомизированными деревьями , Международная конференция по теории и приложениям компьютерного зрения, 2009 г.
1.10.4. Сложность
В общем, время выполнения для построения сбалансированного двоичного дерева составляет $O(n_{samples}n_{features}\log(n_{samples}))$ и время запроса $O(\log(n_{samples}))$. Хотя алгоритм построения дерева пытается генерировать сбалансированные деревья, они не всегда будут сбалансированными. Предполагая, что поддеревья остаются примерно сбалансированными, стоимость на каждом узле состоит из перебора $O(n_{features})$ найти функцию, обеспечивающую наибольшее снижение энтропии. Это стоит $O(n_{features}n_{samples}\log(n_{samples}))$ на каждом узле, что приводит к общей стоимости по всем деревьям (суммируя стоимость на каждом узле) $O(n_{features}n_{samples}^{2}\log(n_{samples}))$
1.10.5. Советы по практическому использованию
- Деревья решений имеют тенденцию чрезмерно соответствовать данным с большим количеством функций. Получение правильного соотношения образцов к количеству функций важно, поскольку дерево с небольшим количеством образцов в многомерном пространстве, скорее всего, переоборудуется.
- Предварительно рассмотрите возможность уменьшения размерности (PCA, ICA, или Feature selection), чтобы дать вашему дереву больше шансов найти отличительные признаки.
- Понимание структуры дерева решений поможет лучше понять, как дерево решений делает прогнозы, что важно для понимания важных функций данных.
- Визуализируйте свое дерево во время тренировки с помощью
exportфункции. Используйтеmax_depth=3в качестве начальной глубины дерева, чтобы понять, насколько дерево соответствует вашим данным, а затем увеличьте глубину. - Помните, что количество образцов, необходимых для заполнения дерева, удваивается для каждого дополнительного уровня, до которого дерево растет. Используйте
max_depthдля управления размером дерева во избежание переобучения. - Используйте
min_samples_splitили,min_samples_leafчтобы гарантировать, что несколько выборок информируют каждое решение в дереве, контролируя, какие разделения будут учитываться. Очень маленькое число обычно означает, что дерево переоборудуется, тогда как большое число не позволяет дереву изучать данные. Попробуйтеmin_samples_leaf=5в качестве начального значения. Если размер выборки сильно различается, в этих двух параметрах можно использовать число с плавающей запятой в процентах. В то время какmin_samples_splitможет создавать произвольно маленькие листья,min_samples_leafгарантирует, что каждый лист имеет минимальный размер, избегая малодисперсных, чрезмерно подходящих листовых узлов в задачах регрессии. Для классификации с несколькими классамиmin_samples_leaf=1это часто лучший выбор.
Обратите внимание, чтоmin_samples_splitвыборки рассматриваются напрямую и независимо от нихsample_weight, если они предусмотрены (например, узел с m взвешенными выборками по-прежнему обрабатывается как имеющий ровно m выборок). Рассмотримmin_weight_fraction_leafилиmin_impurity_decreaseесли учет образцов весов требуются при расколах. - Перед обучением сбалансируйте набор данных, чтобы дерево не смещалось в сторону доминирующих классов. Балансировка классов может быть выполнена путем выборки равного количества выборок из каждого класса или, предпочтительно, путем нормализации суммы весов выборок (
sample_weight) для каждого класса к одному и тому же значению. Также обратите внимание, что критерии предварительного отсечения на основе веса, такие какmin_weight_fraction_leaf, будут менее смещены в сторону доминирующих классов, чем критерии, которые не знают весов выборки, напримерmin_samples_leaf. - Если выборки взвешены, будет проще оптимизировать древовидную структуру, используя основанный на весе критерий предварительной отсечения, например
min_weight_fraction_leaf, который гарантирует, что конечные узлы содержат по крайней мере часть общей суммы весов выборки. - Все деревья решений
np.float32внутренне используют массивы. Если данные обучения не в этом формате, будет сделана копия набора данных. - Если входная матрица X очень разреженная, рекомендуется преобразовать ее в разреженную
csc_matrixперед вызовом соответствия и разреженнуюcsr_matrixперед вызовом предсказания. Время обучения может быть на порядки меньше для входной разреженной матрицы по сравнению с плотной матрицей, когда функции имеют нулевые значения в большинстве выборок.
1.10.6. Алгоритмы дерева: ID3, C4.5, C5.0 и CART
Что представляют собой различные алгоритмы дерева решений и чем они отличаются друг от друга? Какой из них реализован в scikit-learn?
ID3 (Iterative Dichotomiser 3) был разработан Россом Куинланом в 1986 году. Алгоритм создает многостороннее дерево, находя для каждого узла (т. Е. Жадным образом) категориальный признак, который даст наибольший информационный выигрыш для категориальных целей. Деревья вырастают до максимального размера, а затем обычно применяется этап обрезки, чтобы улучшить способность дерева обобщать невидимые данные.
C4.5 является преемником ID3 и снял ограничение, что функции должны быть категориальными, путем динамического определения дискретного атрибута (на основе числовых переменных), который разбивает непрерывное значение атрибута на дискретный набор интервалов. C4.5 преобразует обученные деревья (т. Е. Результат алгоритма ID3) в наборы правил «если-то». Затем оценивается точность каждого правила, чтобы определить порядок, в котором они должны применяться. Удаление выполняется путем удаления предусловия правила, если без него точность правила улучшается.
C5.0 — это последняя версия Quinlan под частной лицензией. Он использует меньше памяти и создает меньшие наборы правил, чем C4.5, но при этом является более точным.
CART (Classification and Regression Trees — деревья классификации и регрессии) очень похож на C4.5, но отличается тем, что поддерживает числовые целевые переменные (регрессию) и не вычисляет наборы правил. CART строит двоичные деревья, используя функцию и порог, которые дают наибольший прирост информации в каждом узле.
scikit-learn использует оптимизированную версию алгоритма CART; однако реализация scikit-learn пока не поддерживает категориальные переменные.
1.10.7. Математическая постановка
Данные обучающие векторы $x_i \in R^n$, i = 1,…, l и вектор-метка $y \in R^l$ дерево решений рекурсивно разбивает пространство признаков таким образом, что образцы с одинаковыми метками или аналогичными целевыми значениями группируются вместе.
Пусть данные в узле m быть представлен $Q_m$ с участием $N_m$ образцы. Для каждого раскола кандидатов $\theta = (j, t_m)$ состоящий из функции $j$ и порог $t_m$, разделите данные на $Q_m^{left}(\theta)$ а также $Q_m^{right}(\theta)$ подмножества
$$Q_m^{left}(\theta) = {(x, y) | x_j <= t_m}$$
$$Q_m^{right}(\theta) = Q_m \setminus Q_m^{left}(\theta)$$
Качество кандидата разделения узла $m$ затем вычисляется с использованием функции примеси или функции потерь $H()$, выбор которых зависит от решаемой задачи (классификация или регрессия)
$$G(Q_m, \theta) = \frac{N_m^{left}}{N_m} H(Q_m^{left}(\theta)) + \frac{N_m^{right}}{N_m} H(Q_m^{right}(\theta))$$
Выберите параметры, которые минимизируют примеси
$$\theta^* = \operatorname{argmin}_\theta G(Q_m, \theta)$$
Рекурсия для подмножеств $Q_m^{left}(\theta^*)$ а также $Q_m^{right}(\theta^*)$ пока не будет достигнута максимально допустимая глубина, $N_m < \min_{samples}$ или же $N_m = 1$.
1.10.7.1. Критерии классификации
Если целью является результат классификации, принимающий значения 0,1,…, K-1, для узла m, позволять
$$p_{mk} = 1/ N_m \sum_{y \in Q_m} I(y = k)$$
быть пропорцией наблюдений класса k в узле m. Еслиmявляется конечным узлом, predict_proba для этого региона установлено значение $p_{mk}$. Общие меры примеси следующие.
Джини:
$$H(Q_m) = \sum_k p_{mk} (1 — p_{mk})$$
Энтропия:
$$H(Q_m) = — \sum_k p_{mk} \log(p_{mk})$$
Неверная классификация:
$$H(Q_m) = 1 — \max(p_{mk})$$
1.10.7.2. Критерии регрессии
Если целью является непрерывное значение, то для узла m, общими критериями, которые необходимо минимизировать для определения местоположений будущих разделений, являются среднеквадратичная ошибка (ошибка MSE или L2), отклонение Пуассона, а также средняя абсолютная ошибка (ошибка MAE или L1). MSE и отклонение Пуассона устанавливают прогнозируемое значение терминальных узлов равным изученному среднему значению $\bar{y}_m$ узла, тогда как MAE устанавливает прогнозируемое значение терминальных узлов равным медиане $median(y)_m$.
Среднеквадратичная ошибка:
$$\bar{y}m = \frac{1}{N_m} \sum{y \in Q_m} y$$
$$H(Q_m) = \frac{1}{N_m} \sum_{y \in Q_m} (y — \bar{y}_m)^2$$
Половинное отклонение Пуассона:
$$H(Q_m) = \frac{1}{N_m} \sum_{y \in Q_m} (y \log\frac{y}{\bar{y}_m} — y + \bar{y}_m)$$
Настройка criterion="poisson" может быть хорошим выбором, если ваша цель — счетчик или частота (количество на какую-то единицу). В любом случае, y>=0 является необходимым условием для использования этого критерия. Обратите внимание, что он подходит намного медленнее, чем критерий MSE.
Средняя абсолютная ошибка:
$$median(y)m = \underset{y \in Q_m}{\mathrm{median}}(y)$$
$$H(Q_m) = \frac{1}{N_m} \sum{y \in Q_m} |y — median(y)_m|$$
Обратите внимание, что он подходит намного медленнее, чем критерий MSE.
1.10.8. Обрезка с минимальными затратами и сложностью
Сокращение с минимальными затратами и сложностью — это алгоритм, используемый для сокращения дерева во избежание чрезмерной подгонки, описанный в главе 3 [BRE] . Этот алгоритм параметризован $\alpha\ge0$ известный как параметр сложности. Параметр сложности используется для определения меры затрат и сложности, $R_\alpha(T)$ данного дерева $T$:
$$R_\alpha(T) = R(T) + \alpha|\widetilde{T}|$$
где $|\widetilde{T}|$ количество конечных узлов в $T$ а также $R(T)$ традиционно определяется как общий коэффициент ошибочной классификации конечных узлов. В качестве альтернативы scikit-learn использует взвешенную общую примесь конечных узлов для $R(T)$. Как показано выше, примесь узла зависит от критерия. Обрезка с минимальными затратами и сложностью находит поддеревоT что сводит к минимуму $R_\alpha(T)$.
Оценка сложности стоимости одного узла составляет $R_\alpha(t)=R(t)+\alpha$. Ответвление $T_t$, определяется как дерево, в котором узел $t$ это его корень. В общем, примесь узла больше, чем сумма примесей его конечных узлов, $R(T_t)<R(t)$. Однако мера стоимости и сложности узла, $t$, и его ветвь, $T_t$, может быть равным в зависимости от $\alpha$. Определяем эффективныйα узла быть значением, где они равны, $R_\alpha(T_t)=R_\alpha(t)$ или же $\alpha_{eff}(t)=\frac{R(t)-R(T_t)}{|T|-1}$. Нетерминальный узел с наименьшим значением $\alpha_{eff}$ является самым слабым звеном и будет удалено. Этот процесс останавливается, когда обрезанное дерево минимально $\alpha_{eff}$ больше ccp_alpha параметра.
Рекомендации:
- BRE Л. Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984.
- https://en.wikipedia.org/wiki/Decision_tree_learning
- https://en.wikipedia.org/wiki/Predictive_analytics
- JR Quinlan. C4. 5: программы для машинного обучения. Морган Кауфманн, 1993.
- Т. Хасти, Р. Тибширани и Дж. Фридман. Элементы статистического обучения, Springer, 2009.
