1.12. Мультиклассовые и множественные алгоритмы вывода ¶
Этот раздел пользователя функциональность руководство охватывает связанный с мульти-обучением проблем, в том числе мультиклассирует , MultiLabel и multioutput классификации и регрессии.
Модули в этом разделе реализуют мета-оценки , для которых требуется, чтобы в их конструкторе была указана базовая оценка. Мета-оценки расширяют функциональные возможности базовой оценки для поддержки задач с множественным обучением, что достигается путем преобразования задачи с множественным обучением в набор более простых задач, а затем подгонки одного оценщика для каждой задачи.
В этом разделе рассматриваются два модуля: sklearn.multiclass и sklearn.multioutput. В приведенной ниже таблице показаны типы проблем, за которые отвечает каждый модуль, и соответствующие метаоценки, которые предоставляет каждый модуль.
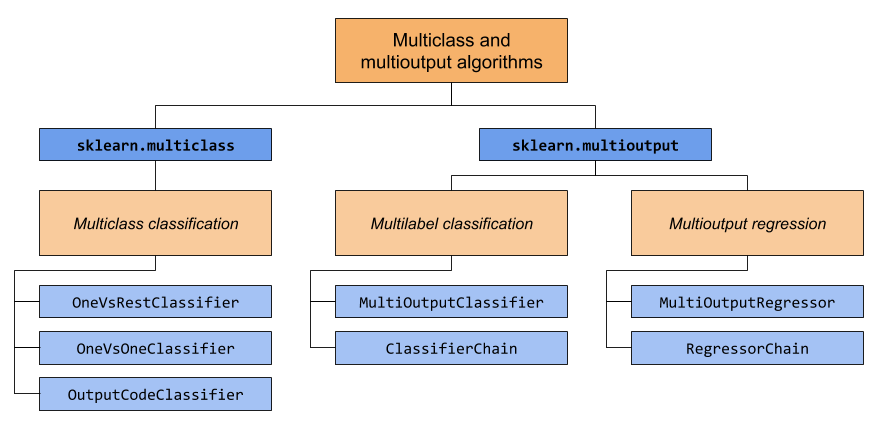
В таблице ниже приведены краткие сведения о различиях между типами проблем. Более подробные объяснения можно найти в следующих разделах этого руководства.
| Количество целей | Целевая мощность | Действительныйtype_of_target | |
| Мультиклассовая классификация | 1 | >2 | ‘мультикласс’ |
| Классификация по нескольким этикеткам | >1 | 2 (0 или 1) | ‘многозначный-индикатор’ |
| Классификация нескольких классов и нескольких выходов | >1 | >2 | ‘мультикласс-мульти-выход’ |
| Регрессия с несколькими выходами | >1 | Непрерывный | ‘непрерывно-множественный выход’ |
Ниже приводится сводка оценщиков scikit-learn, которые имеют встроенную поддержку множественного обучения, сгруппированных по стратегиям. Вам не нужны мета-оценщики, представленные в этом разделе, если вы используете одну из этих оценщиков. Однако метаоценки могут предоставить дополнительные стратегии помимо встроенных:
- По своей сути мультикласс:
naive_bayes.BernoulliNBtree.DecisionTreeClassifiertree.ExtraTreeClassifierensemble.ExtraTreesClassifiernaive_bayes.GaussianNBneighbors.KNeighborsClassifiersemi_supervised.LabelPropagationsemi_supervised.LabelSpreadingdiscriminant_analysis.LinearDiscriminantAnalysissvm.LinearSVC(setting multi_class=”crammer_singer”)linear_model.LogisticRegression(setting multi_class=”multinomial”)linear_model.LogisticRegressionCV(setting multi_class=”multinomial”)neural_network.MLPClassifierneighbors.NearestCentroiddiscriminant_analysis.QuadraticDiscriminantAnalysisneighbors.RadiusNeighborsClassifierensemble.RandomForestClassifierlinear_model.RidgeClassifierlinear_model.RidgeClassifierCV
- Мультикласс как One-Vs-One:
svm.NuSVCsvm.SVC.gaussian_process.GaussianProcessClassifier(setting multi_class = “one_vs_one”)
- Мультикласс как один против остальных:
ensemble.GradientBoostingClassifiergaussian_process.GaussianProcessClassifier(setting multi_class = “one_vs_rest”)svm.LinearSVC(setting multi_class=”ovr”)linear_model.LogisticRegression(setting multi_class=”ovr”)linear_model.LogisticRegressionCV(setting multi_class=”ovr”)linear_model.SGDClassifierlinear_model.Perceptronlinear_model.PassiveAggressiveClassifier
- Поддержка нескольких ярлыков:
- Поддержка мультикласса-множественного вывода:
1.12.1. Мультиклассовая классификация
Предупреждение
Все классификаторы в scikit-learn делают мультиклассовую классификацию «из коробки». Вам не нужно использовать sklearn.multiclass модуль, если вы не хотите экспериментировать с различными мультиклассовыми стратегиями.
Мультиклассовая классификация — это задача классификации с более чем двумя классами. Каждый образец можно пометить только как один класс.
Например, классификация с использованием признаков, извлеченных из набора изображений фруктов, где каждое изображение может быть апельсином, яблоком или грушей. Каждое изображение представляет собой один образец и помечен как один из 3 возможных классов. Мультиклассовая классификация предполагает, что каждому образцу присваивается одна и только одна метка — например, один образец не может быть одновременно грушей и яблоком.
Хотя все классификаторы scikit-learn способны к многоклассовой классификации, предлагаемые метаоценки sklearn.multiclass позволяют изменять способ обработки более двух классов, потому что это может повлиять на производительность классификатора (либо с точки зрения ошибки обобщения, либо с точки зрения требуемых вычислительных ресурсов).
1.12.1.1. Целевой формат
Допустимые мультиклассовые представления для type_of_target(y):
- 1d или вектор-столбец, содержащий более двух дискретных значений. Пример вектора
yдля 4-х отсчетов:
>>> import numpy as np >>> y = np.array(['apple', 'pear', 'apple', 'orange']) >>> print(y) ['apple' 'pear' 'apple' 'orange']
- Плотная или разреженная двоичная матрица формы (n_samples, n_classes) с одним образцом в строке, где каждый столбец представляет один класс. Пример как плотной, так и разреженной двоичной матрицы y для 4 образцов, где столбцы по порядку — яблоко, апельсин и груша:
>>> import numpy as np
>>> from sklearn.preprocessing import LabelBinarizer
>>> y = np.array(['apple', 'pear', 'apple', 'orange'])
>>> y_dense = LabelBinarizer().fit_transform(y)
>>> print(y_dense)
[[1 0 0]
[0 0 1]
[1 0 0]
[0 1 0]]
>>> from scipy import sparse
>>> y_sparse = sparse.csr_matrix(y_dense)
>>> print(y_sparse)
(0, 0) 1
(1, 2) 1
(2, 0) 1
(3, 1) 1Для получения дополнительной информации LabelBinarizer обратитесь к Преобразованию цели прогноза (y) .
1.12.1.2. OneVsRestClassifier
Один-против-остальных (one-vs-rest) стратегии, также известный как один-против-всех , реализуется OneVsRestClassifier. Стратегия заключается в подборе одного классификатора на класс. Для каждого классификатора класс сопоставляется со всеми другими классами. Помимо вычислительной эффективности ( n_classes нужны только классификаторы), одним из преимуществ этого подхода является его интерпретируемость. Поскольку каждый класс представлен одним и только одним классификатором, можно получить информацию о классе, проверив соответствующий классификатор. Это наиболее часто используемая стратегия и справедливый выбор по умолчанию.
Ниже приведен пример мультиклассового обучения с использованием OvR:
>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsRestClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> OneVsRestClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])OneVsRestClassifier также поддерживает многозначную классификацию. Чтобы использовать эту функцию, загрузите в классификатор индикаторную матрицу, в которой ячейка [i, j] указывает наличие метки j в образце i.
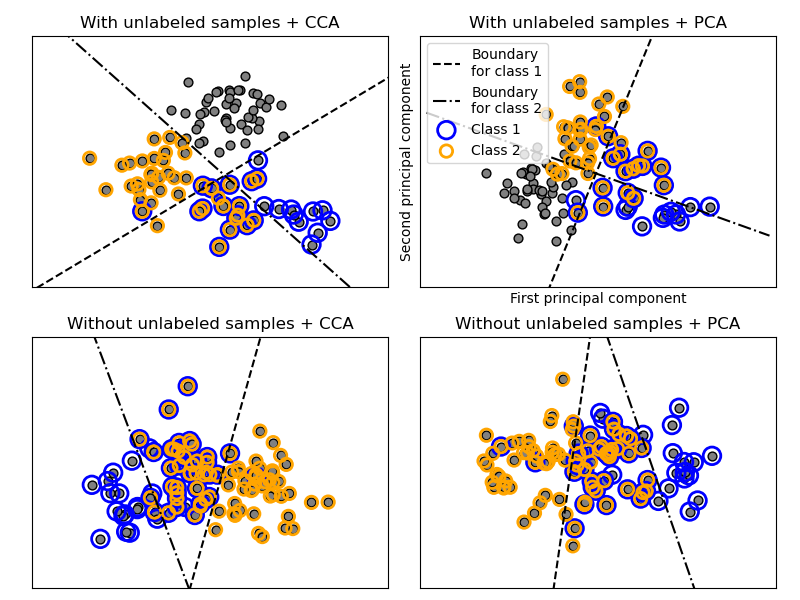
1.12.1.3. OneVsOneClassifier
OneVsOneClassifier создает один классификатор на пару классов. Во время прогнозирования выбирается класс, получивший наибольшее количество голосов. В случае равенства голосов (среди двух классов с равным количеством голосов) он выбирает класс с наивысшей совокупной достоверностью классификации путем суммирования уровней достоверности попарной классификации, вычисленных базовыми двоичными классификаторами.
Поскольку он требует соответствия n_classes * (n_classes — 1) / 2 классификаторам, этот метод обычно медленнее, чем метод «один против остальных» из-за его сложности O (n_classes ^ 2). Однако этот метод может быть полезен для таких алгоритмов, как алгоритмы ядра, которые плохо масштабируются с n_samples. Это связано с тем, что каждая отдельная задача обучения включает только небольшое подмножество данных, тогда как при использовании одного или остальных данных используется весь набор данных несколько n_classes раз. Решающая функция является результатом монотонного преобразования однозначной классификации.
Ниже приведен пример мультиклассового обучения с использованием OvO:
>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsOneClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> OneVsOneClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])Рекомендации
- «Распознавание образов и машинное обучение. Springer », Кристофер М. Бишоп, стр. 183, (Первое издание)
1.12.1.4. OutputCodeClassifier
Стратегии на основе выходного кода с исправлением ошибок сильно отличаются от стратегий «один против остальных» и «один против одного». С помощью этих стратегий каждый класс представлен в евклидовом пространстве, где каждое измерение может быть только 0 или 1. Другими словами, каждый класс представлен двоичным кодом (массивом из 0 и 1). Матрица, которая отслеживает местоположение / код каждого класса, называется кодовой книгой. Размер кода — это размерность вышеупомянутого пространства. Интуитивно каждый класс должен быть представлен как можно более уникальным кодом, и должна быть разработана хорошая кодовая книга для оптимизации точности классификации. В этой реализации мы просто используем случайно сгенерированную кодовую книгу, как рекомендовано в 3, хотя в будущем могут быть добавлены более сложные методы.
Во время подгонки устанавливается один двоичный классификатор на бит в кодовой книге. Во время прогнозирования классификаторы используются для проецирования новых точек в пространстве классов, и выбирается класс, ближайший к этим точкам.
В OutputCodeClassifier, то code_size атрибут позволяет пользователю контролировать количество классификаторов , которые будут использоваться. Это процент от общего количества занятий.
Число от 0 до 1 потребует меньшего количества классификаторов, чем один по сравнению с остальными. Теоретически log2(n_classes) / n_classes этого достаточно, чтобы однозначно представить каждый класс. Однако на практике это может не привести к хорошей точности, поскольку log2(n_classes) намного меньше, чем n_classes.
Число больше 1 потребует больше классификаторов, чем один против остальных. В этом случае некоторые классификаторы теоретически исправят ошибки, допущенные другими классификаторами, отсюда и название «исправляющие ошибки». Однако на практике этого может не произойти, поскольку ошибки классификатора обычно коррелируют. Коды вывода с исправлением ошибок имеют тот же эффект, что и упаковка.
Ниже приведен пример мультиклассового обучения с использованием выходных кодов:
>>> from sklearn import datasets
>>> from sklearn.multiclass import OutputCodeClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> clf = OutputCodeClassifier(LinearSVC(random_state=0),
... code_size=2, random_state=0)
>>> clf.fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1,
1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 1, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])Рекомендации
- «Решение задач мультиклассового обучения с помощью выходных кодов с исправлением ошибок», Диттерих Т., Бакири Г., Журнал исследований искусственного интеллекта 2, 1995.
- 3 «Метод кодирования ошибок и PICT», Джеймс Г., Хасти Т., Журнал вычислительной и графической статистики 7, 1998.
- «Элементы статистического обучения», Хасти Т., Тибширани Р., Фридман Дж., Стр. 606 (второе издание) 2008 г.
1.12.2. Классификация по нескольким меткам
Классификация с несколькими метками (тесно связана с классификацией с несколькими выходами ) — это задача классификации, при которой каждый образец m маркируется метками из n_classes возможных классов, где m может быть от 0 до n_classes включительно. Это можно рассматривать как прогнозирование свойств образца, которые не исключают друг друга. Формально двоичный вывод назначается каждому классу для каждой выборки. Положительные классы обозначаются цифрой 1, а отрицательные классы — 0 или -1. Таким образом, это сравнимо с запуском n_classes задач двоичной классификации, например, с MultiOutputClassifier. Этот подход обрабатывает каждую метку независимо, тогда как классификаторы с несколькими метками могут обрабатывать несколько классов одновременно, учитывая коррелированное поведение между ними.
Например, предсказание тем, относящихся к текстовому документу или видео. Документ или видео могут быть посвящены одному из следующих: «религия», «политика», «финансы» или «образование», несколько тематических классов или все тематические классы.
1.12.2.1. Целевой формат
Допустимым представлением множественной метки y является либо плотная, либо разреженная двоичная матрица формы (n_samples, n_classes). Каждый столбец представляет класс. Первый в каждой строке обозначают положительные классов образец был меченные. Пример плотной матрицы y на 3 образца:
>>> y = np.array([[1, 0, 0, 1], [0, 0, 1, 1], [0, 0, 0, 0]]) >>> print(y) [[1 0 0 1] [0 0 1 1] [0 0 0 0]]
Плотные двоичные матрицы также могут быть созданы с помощью MultiLabelBinarizer. Для получения дополнительной информации обратитесь к Преобразованию цели прогноза (y) .
Пример того же yв разреженной матричной форме:
>>> y_sparse = sparse.csr_matrix(y) >>> print(y_sparse) (0, 0) 1 (0, 3) 1 (1, 2) 1 (1, 3) 1
1.12.2.2. MultiOutputClassifier
Поддержка классификации с несколькими метками может быть добавлена к любому классификатору с помощью MultiOutputClassifier. Эта стратегия состоит из подбора одного классификатора для каждой цели. Это позволяет несколько классификаций целевых переменных. Цель этого класса — расширить оценщики, чтобы иметь возможность оценивать серию целевых функций (f1, f2, f3…, fn), которые обучены на одной матрице предикторов X, чтобы предсказать серию ответов (y1, y2, y3 …, Уп).
Ниже приведен пример классификации по множеству ярлыков:
>>> from sklearn.datasets import make_classification
>>> from sklearn.multioutput import MultiOutputClassifier
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.utils import shuffle
>>> import numpy as np
>>> X, y1 = make_classification(n_samples=10, n_features=100, n_informative=30, n_classes=3, random_state=1)
>>> y2 = shuffle(y1, random_state=1)
>>> y3 = shuffle(y1, random_state=2)
>>> Y = np.vstack((y1, y2, y3)).T
>>> n_samples, n_features = X.shape # 10,100
>>> n_outputs = Y.shape[1] # 3
>>> n_classes = 3
>>> forest = RandomForestClassifier(random_state=1)
>>> multi_target_forest = MultiOutputClassifier(forest, n_jobs=-1)
>>> multi_target_forest.fit(X, Y).predict(X)
array([[2, 2, 0],
[1, 2, 1],
[2, 1, 0],
[0, 0, 2],
[0, 2, 1],
[0, 0, 2],
[1, 1, 0],
[1, 1, 1],
[0, 0, 2],
[2, 0, 0]])1.12.2.3. ClassifierChain
Цепочки классификаторов (см. ClassifierChain) — это способ объединения ряда бинарных классификаторов в единую модель с несколькими метками, которая способна использовать корреляции между целями.
Для задачи классификации с несколькими метками с N классами N двоичным классификаторам присваивается целое число от 0 до N-1. Эти целые числа определяют порядок моделей в цепочке. Затем каждый классификатор соответствует доступным обучающим данным плюс истинным меткам классов, моделям которых был присвоен меньший номер.
При прогнозировании истинные метки будут недоступны. Вместо этого прогнозы каждой модели передаются последующим моделям в цепочке для использования в качестве функций.
Ясно, что порядок цепочки важен. Первая модель в цепочке не имеет информации о других метках, в то время как последняя модель в цепочке имеет признаки, указывающие на наличие всех других меток. Как правило, неизвестен оптимальный порядок моделей в цепочке, поэтому обычно подбирается много случайно упорядоченных цепочек, а их прогнозы усредняются вместе.
Рекомендации
- Джесси Рид, Бернхард Пфарингер, Джефф Холмс, Эйбе Франк, «Цепочки классификаторов для многокомпонентной классификации», 2009 г.
1.12.3. Классификация многоклассов и нескольких выходов
Классификация по нескольким классам и множеству выходов (также известная как многозадачная классификация ) — это задача классификации, которая маркирует каждый образец набором недвоичных свойств. И количество свойств, и количество классов для каждого свойства больше 2. Таким образом, один оценщик обрабатывает несколько совместных задач классификации. Это как обобщение задачи классификации нескольких меток , которая учитывает только двоичные атрибуты, так и обобщение задачи классификации нескольких классов , в которой рассматривается только одно свойство.
Например, классификация свойств «вид фрукта» и «цвет» для набора изображений фруктов. Свойство «вид фрукта» имеет возможные классы: «яблоко», «груша» и «апельсин». Свойство «цвет» имеет возможные классы: «зеленый», «красный», «желтый» и «оранжевый». Каждый образец представляет собой изображение фрукта, метка выводится для обоих свойств, и каждая метка является одним из возможных классов соответствующего свойства.
Обратите внимание на то, что все классификаторы, обрабатывающие задачи многоклассового вывода (также известные как многозадачная классификация), поддерживают задачу многоклассовой классификации как особый случай. Классификация многозадачности аналогична задаче классификации с несколькими выходами с различными формулировками модели. Для получения дополнительной информации см. Соответствующую документацию оценщика.
Предупреждение
В настоящее время ни одна метрика не sklearn.metrics поддерживает задачу классификации нескольких классов и нескольких выходов.
1.12.3.1. Целевой формат
Допустимое представление множественного вывода y — это плотная матрица формы (n_samples, n_classes) меток классов. Конкатенация по столбцам 1d мультиклассовых переменных. Пример y для 3-х образцов:
>>> y = np.array([['apple', 'green'], ['orange', 'orange'], ['pear', 'green']]) >>> print(y) [['apple' 'green'] ['orange' 'orange'] ['pear' 'green']]
1.12.4. Регрессия с несколькими выходами
Регрессия с несколькими выходами предсказывает несколько числовых свойств для каждой выборки. Каждое свойство представляет собой числовую переменную, и количество свойств, которые должны быть предсказаны для каждой выборки, больше или равно 2. Некоторые оценщики, поддерживающие регрессию с несколькими выходами, работают быстрее, чем просто выполняемые n_output оценщики.
Например, прогнозирование скорости и направления ветра в градусах с использованием данных, полученных в определенном месте. Каждая выборка будет данными, полученными в одном месте, и скорость и направление ветра будут выводиться для каждой выборки.
1.12.4.1. Целевой формат
Правильное представление множественного вывода y — это плотная матрица формы (n_samples, n_classes) поплавков. Конкатенация непрерывных переменных по столбцам . Пример y для 3-х образцов:
>>> y = np.array([[31.4, 94], [40.5, 109], [25.0, 30]]) >>> print(y) [[ 31.4 94. ] [ 40.5 109. ] [ 25. 30. ]]
1.12.4.2. MultiOutputRegressor
Поддержка множественной регрессии может быть добавлена к любому регрессору с помощью MultiOutputRegressor. Эта стратегия состоит из подбора одного регрессора для каждой цели. Поскольку каждая цель представлена ровно одним регрессором, можно получить информацию о цели, проверив соответствующий регрессор. Поскольку MultiOutputRegressor для каждой цели используется один регрессор, он не может использовать корреляции между целями.
Ниже приведен пример регрессии с несколькими выходами:
>>> from sklearn.datasets import make_regression
>>> from sklearn.multioutput import MultiOutputRegressor
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_regression(n_samples=10, n_targets=3, random_state=1)
>>> MultiOutputRegressor(GradientBoostingRegressor(random_state=0)).fit(X, y).predict(X)
array([[-154.75474165, -147.03498585, -50.03812219],
[ 7.12165031, 5.12914884, -81.46081961],
[-187.8948621 , -100.44373091, 13.88978285],
[-141.62745778, 95.02891072, -191.48204257],
[ 97.03260883, 165.34867495, 139.52003279],
[ 123.92529176, 21.25719016, -7.84253 ],
[-122.25193977, -85.16443186, -107.12274212],
[ -30.170388 , -94.80956739, 12.16979946],
[ 140.72667194, 176.50941682, -17.50447799],
[ 149.37967282, -81.15699552, -5.72850319]])1.12.4.3. RegressorChain
Цепочки регрессоров (см. RegressorChain) Аналогичны ClassifierChain способу объединения ряда регрессий в единую многоцелевую модель, способную использовать корреляции между целями.
