1.14. Полу-контролируемое обучение ¶

Полу-контролируемое обучение — это ситуация, в которой в ваших обучающих данных некоторые образцы не помечены. Полуконтролируемые оценщики в sklearn.semi_supervised могут использовать эти дополнительные немаркированные данные, чтобы лучше фиксировать форму основного распределения данных и лучше обобщать для новых выборок. Эти алгоритмы могут работать хорошо, когда у нас очень небольшое количество помеченных точек и большое количество немаркированных точек.

1.14.1. Самостоятельное обучение

Эта реализация самообучения основана на алгоритме Яровского 1 . Используя этот алгоритм, данный контролируемый классификатор может функционировать как полууправляемый классификатор, позволяя ему учиться на немаркированных данных.

SelfTrainingClassifier может быть вызван с любым классификатором, который реализует predict_proba, переданным в качестве параметра base_classifier. На каждой итерации base_classifier прогнозирует метки для немаркированных выборок и добавляет подмножество этих меток в помеченный набор данных.

Выбор этого подмножества определяется критерием отбора. Этот выбор может быть выполнен с использованием threshold вероятностей предсказания или путем выбора k_best выборок в соответствии с вероятностями предсказания.

Метки, используемые для окончательной подгонки, а также итерация, в которой был помечен каждый образец, доступны как атрибуты. Необязательный max_iter параметр указывает, сколько раз цикл выполняется максимум.

Параметр max_iter может быть установлен None, в результате чего алгоритма итерации , пока все образцы не имеют меток или никаких новые образцы не будут выбраны в этой итерации.

1.14.2. Распространение метки

Распространение метки обозначает несколько вариантов алгоритмов вывода полууправляемых графов.В этой модели доступны несколько функций:

• Используется для задач классификации
• Методы ядра для проецирования данных в альтернативные размерные пространства

scikit-learn предоставляет две модели распространения меток: LabelPropagation и LabelSpreading. Оба работают путем построения графа сходства по всем элементам входного набора данных.

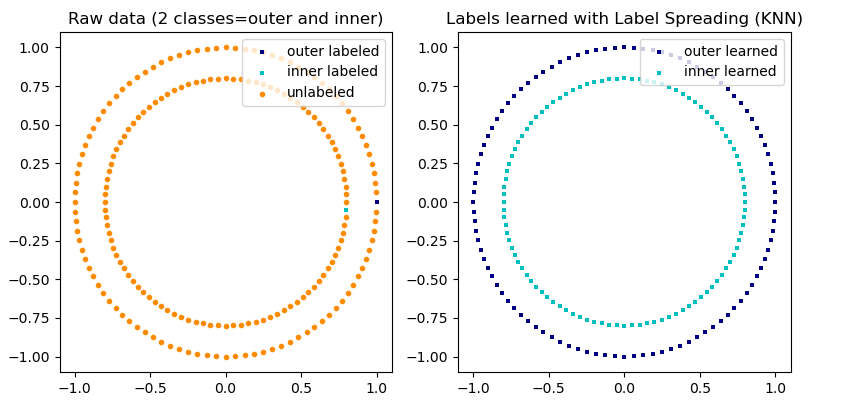
Иллюстрация распространения метки: структура немаркированных наблюдений согласуется со структурой класса, и, таким образом, метка класса может быть распространена на немаркированные наблюдения обучающего набора.

LabelPropagation и LabelSpreadingотличаются модификациями матрицы сходства, которая графически отображается, и эффектом ограничения на распределения меток. Фиксация позволяет алгоритму до некоторой степени изменять вес данных, помеченных истинной землей. Алгоритм LabelPropagation выполняет жесткий зажим входных меток, что означает $\alpha=0$. Этот ограничивающий фактор можно ослабить, например $\alpha=0.2$, что означает, что мы всегда будем сохранять 80 процентов нашего исходного распределения меток, но алгоритм может изменить свою уверенность в распределении в пределах 20 процентов.

LabelPropagation использует исходную матрицу сходства, построенную на основе данных без каких-либо модификаций. Напротив, LabelSpreading минимизирует функцию потерь, которая имеет свойства регуляризации, как таковая часто более устойчива к шуму. Алгоритм выполняет итерацию по модифицированной версии исходного графа и нормализует веса ребер, вычисляя матрицу лапласиана нормализованного графа. Эта процедура также используется в спектральной кластеризации .

В моделях распространения меток есть два встроенных метода ядра. Выбор ядра влияет как на масштабируемость, так и на производительность алгоритмов. Доступны следующие варианты:

• rbf ($\exp(-\gamma |x-y|^2), \gamma > 0$). $\gamma$ определяется ключевым словом гамма.
• knn ($1[x’ \in kNN(x)]$). $k$ определяется ключевым словом n_neighbors.

Ядро RBF будет создавать полносвязный граф, который представлен в памяти плотной матрицей. Эта матрица может быть очень большой и в сочетании с затратами на выполнение вычисления полного матричного умножения для каждой итерации алгоритма может привести к недопустимо долгому времени выполнения. С другой стороны, ядро ​​KNN будет создавать гораздо более удобную для памяти разреженную матрицу, которая может значительно сократить время работы.