1.2. Линейный и квадратичный дискриминантный анализ ¶

Линейный дискриминантный анализ ( LinearDiscriminantAnalysis) и квадратичный дискриминантный анализ ( QuadraticDiscriminantAnalysis) — это два классических классификатора с, как следует из их названия, линейной и квадратичной поверхностью принятия решений соответственно.

Эти классификаторы привлекательны тем, что у них есть решения в замкнутой форме, которые можно легко вычислить, они по своей сути являются мультиклассами, доказали свою эффективность на практике и не имеют гиперпараметров для настройки.

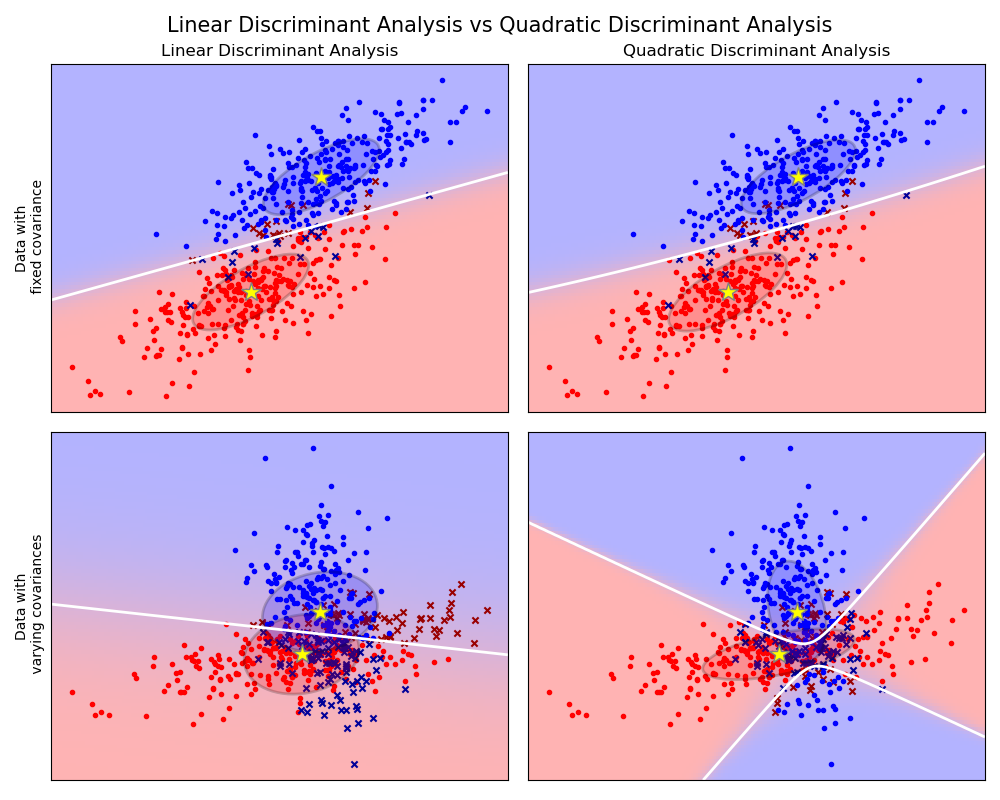
График показывает границы решения для линейного дискриминантного анализа и квадратичного дискриминантного анализа. Нижняя строка демонстрирует, что линейный дискриминантный анализ может изучать только линейные границы, в то время как квадратичный дискриминантный анализ может изучать квадратичные границы и, следовательно, более гибкий.

1.2.1. Снижение размерности с помощью линейного дискриминантного анализа

LinearDiscriminantAnalysis может использоваться для выполнения контролируемого уменьшения размерности путем проецирования входных данных на линейное подпространство, состоящее из направлений, которые максимизируют разделение между классами (в точном смысле, обсуждаемом в разделе математики ниже). Размерность вывода обязательно меньше, чем количество классов, так что в целом это довольно сильное снижение размерности и имеет смысл только в мультиклассовой настройке.

Это реализовано в transform методе. Желаемую размерность можно установить с помощью n_components параметра. Этот параметр не имеет никакого влияния на fit и predict методы.

1.2.2. Математическая формулировка классификаторов LDA и QDA

И LDA, и QDA могут быть получены из простых вероятностных моделей, которые моделируют условное распределение данных по классам. $P(X|y=k)$ для каждого класса $k$. Затем прогнозы могут быть получены с использованием правила Байеса для каждой обучающей выборки.$x \in $R^d$:
$$P(y=k | x) = \frac{P(x | y=k) P(y=k)}{P(x)} = \frac{P(x | y=k) P(y = k)}{ \sum_{l} P(x | y=l) \cdot P(y=l)}$$

и выбираем класс $k$ что максимизирует эту апостериорную вероятность.

В частности, для линейного и квадратичного дискриминантного анализа $P(x|y)$ моделируется многомерным распределением Гаусса с плотностью:
$$P(x | y=k) = \frac{1}{(2\pi)^{d/2} |\Sigma_k|^{1/2}}\exp\left(-\frac{1}{2} (x-\mu_k)^t \Sigma_k^{-1} (x-\mu_k)\right)$$

где $d$ количество функций.

1.2.2.1. QDA

Согласно модели, приведенной выше, бревно заднего отдела выглядит следующим образом:

$$\begin{split}\log P(y=k | x) &= \log P(x | y=k) + \log P(y = k) + Cst \ &= -\frac{1}{2} \log |\Sigma_k| -\frac{1}{2} (x-\mu_k)^t \Sigma_k^{-1} (x-\mu_k) + \log P(y = k) + Cst,\end{split}$$

где постоянный член $C_{st}$ соответствует знаменателю $P(x)$, в дополнение к другим постоянным членам из гауссиана. Прогнозируемый класс — это тот, который максимизирует этот логарифмический апостериор.

1.2.2.2. LDA

LDA — это частный случай QDA, где предполагается, что гауссианы для каждого класса имеют одну и ту же ковариационную матрицу: $\Sigma_k = \Sigma$ для всех $k$. Это уменьшает размер журнала до:
$$\log P(y=k | x) = -\frac{1}{2} (x-\mu_k)^t \Sigma^{-1} (x-\mu_k) + \log P(y = k) + Cst.$$

Термин $(x-\mu_k)^t \Sigma^{-1} (x-\mu_k)$ соответствует расстоянию Махаланобиса между образцамиx и среднее $\mu_k$. Расстояние Махаланобиса показывает, насколько близко $x$ из $\mu_k$, а также учитывает дисперсию каждой функции. Таким образом, мы можем интерпретировать LDA как присвоение $x$ к классу, среднее значение которого является наиболее близким с точки зрения расстояния Махаланобиса, с учетом априорных вероятностей класса.

Лог-апостериор LDA также можно записать (Источник 3) как:
$$\log P(y=k | x) = \omega_k^t x + \omega_{k0} + Cst.$$

где $\omega_k = \Sigma^{-1} \mu_k$ и $\omega_{k0} =-\frac{1}{2} \mu_k^t\Sigma^{-1}\mu_k + \log P (y = k)$. Эти величины соответствуют coef_и intercept_ атрибутам, соответственно.

Из приведенной выше формулы ясно, что LDA имеет линейную поверхность принятия решений. В случае QDA нет никаких предположений о ковариационных матрицах $\Sigma_k$ гауссианов, что приводит к квадратичным решающим поверхностям. См. (Источник 1) для более подробной информации.

1.2.3. Математическая формулировка уменьшения размерности LDA

Сначала обратите внимание, что K означает $\mu_k$ векторы в $R^d$, и они лежат в аффинном подпространстве $H$ размер не более $K−1$ (2 точки лежат на прямой, 3 точки лежат на плоскости и т. Д.).

Как упоминалось выше, мы можем интерпретировать LDA как присвоение x классу, средний $\mu_k$ является ближайшим с точки зрения расстояния Махаланобиса с учетом априорных вероятностей класса. В качестве альтернативы LDA эквивалентно сначала сферированию данных, так что ковариационная матрица является тождественной, а затем назначению $x$ к ближайшему среднему с точки зрения евклидова расстояния (все еще с учетом априорных значений класса).

Вычисление евклидовых расстояний в этом d-мерном пространстве эквивалентно первому проецированию точек данных в $H$, и вычисление расстояний там (поскольку другие измерения будут одинаково влиять на каждый класс с точки зрения расстояния). Другими словами, еслиx ближе всего к $\mu_k$ в исходном пространстве, то же самое будет и в $H$. Это показывает, что, неявно в классификаторе LDA, происходит уменьшение размерности за счет линейной проекции на $K−1$ пространственное пространство.

Мы можем уменьшить размер еще больше, до выбранного $L$, проецируя на линейное подпространство $H_L$ что максимизирует дисперсию $\mu_{k}^{*}$ после проекции (по сути, мы выполняем форму PCA для преобразованных средств класса $\mu^*_k$). Этот $L$ соответствует n_components параметру, используемому в transform методе. См. (Источник 1) для более подробной информации.

1.2.4. Оценка усадки и ковариации

Сжатие — это форма регуляризации, используемая для улучшения оценки ковариационных матриц в ситуациях, когда количество обучающих выборок мало по сравнению с количеством функций. В этом сценарии ковариация эмпирической выборки является плохой оценкой, а сжатие помогает улучшить характеристики обобщения классификатора. LDA усадки можно использовать, установив для shrinkage параметра LinearDiscriminantAnalysis класса значение «auto». Это автоматически определяет оптимальный параметр усадки аналитическим способом, следуя лемме, введенной Ледуа и Вольфом (Источник 2) . Обратите внимание, что в настоящее время сжатие работает только при установке solver параметра на «lsqr» или «eigen».

Параметр shrinkage также можно вручную установить между 0 и 1. В частности, значение 0 соответствует отсутствию усадки (что означает эмпирической ковариационной матрицы будет использоваться) , и значение 1 соответствует полной усадки (что означает , что диагональная матрица дисперсий будет использоваться в качестве оценки ковариационной матрицы). Установка для этого параметра значения между этими двумя экстремумами будет оценивать сокращенную версию ковариационной матрицы.

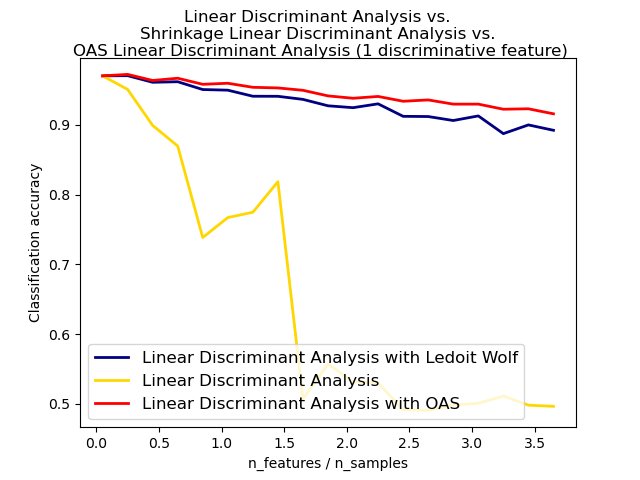
Сжатая оценка ковариации Ледуа и Вольфа не всегда может быть лучшим выбором. Например, если распределение данных является нормальным, оценка Oracle Shrinkage Approximating sklearn.covariance.OAS дает меньшую среднеквадратичную ошибку, чем та, которую дает формула Ледуа и Вольфа, используемая с shrinkage = ”auto”. В LDA предполагается, что данные являются гауссовскими условно для класса. Если эти предположения верны, использование LDA с оценкой ковариации OAS даст лучшую точность классификации, чем использование Ледуа и Вольфа или эмпирической оценки ковариации.

Оценщик ковариации можно выбрать с помощью covariance_estimator параметра discriminant_analysis.LinearDiscriminantAnalysis класса. Оценщик ковариации должен иметь метод соответствия и covariance_ атрибут, как и все оценщики ковариации в sklearn.covariance модуле.

1.2.5. Алгоритмы оценивания

Использование LDA и QDA требует вычисления логарифмической апостериорной функции, которая зависит от априорных значений класса. $P(y=k)$, класс означает $\mu_k$, и ковариационные матрицы.

The ‘svd’ solver is the default solver used for LinearDiscriminantAnalysis, and it is the only available solver for QuadraticDiscriminantAnalysis. It can perform both classification and transform (for LDA). As it does not rely on the calculation of the covariance matrix, the ‘svd’ solver may be preferable in situations where the number of features is large. The ‘svd’ solver cannot be used with shrinkage. For QDA, the use of the SVD solver relies on the fact that the covariance matrix $\Sigma_k$ is, by definition, equal to $\frac{1}{n — 1}X_k^tX_k = V S^2 V^t$ where $V$ comes from the SVD of the (centered) matrix: $X_k = U S V^t$. It turns out that we can compute the log-posterior above without having to explictly compute $\Sigma$: computing $S$ and $V$ via the SVD of $X$ is enough. For LDA, two SVDs are computed: the SVD of the centered input matrix $X$ and the SVD of the class-wise mean vectors.

Решающая программа lsqr — это эффективный алгоритм, который работает только для классификации. Необходимо явно вычислить ковариационную матрицу $\Sigma$, а также поддерживает оценки усадки и пользовательские оценки ковариации. Этот решатель вычисляет коэффициенты $\omega_k = \Sigma^{-1}\mu_k$ решая для $\Sigma \omega =\mu_k$, что позволяет избежать явного вычисления обратного $\Sigma^{-1}$.

«Собственный» решатель основан на оптимизации разброса между классами до коэффициента разброса внутри классов. Его можно использовать как для классификации, так и для преобразования, и он поддерживает сжатие. Однако «собственный» решатель должен вычислять ковариационную матрицу, поэтому он может не подходить для ситуаций с большим количеством функций.