1.3. Регрессия гребня ядра ¶

Регрессия гребня ядра (KRR) [M2012] сочетает в себе регрессию и классификацию Риджа (линейный метод наименьших квадратов с регуляризацией по l2-норме) с уловкой ядра . Таким образом, он изучает линейную функцию в пространстве, индуцированную соответствующим ядром и данными. Для нелинейных ядер это соответствует нелинейной функции в исходном пространстве.

Форма модели, которую изучил, KernelRidge идентична форме поддержки векторной регрессии (SVR). Однако используются другие функции потерь: KRR использует квадратичную потерю ошибок, в то время как опорная векторная регрессия используетϵ-нечувствительные потери в сочетании с регуляризацией l2. В отличие от этого SVR, подгонка KernelRidge может выполняться в закрытой форме и обычно быстрее для наборов данных среднего размера. С другой стороны, изученная модель не является разреженной и, следовательно, медленнее, чем SVR, которая изучает разреженную модель для $\epsilon > 0$, во время предсказания.

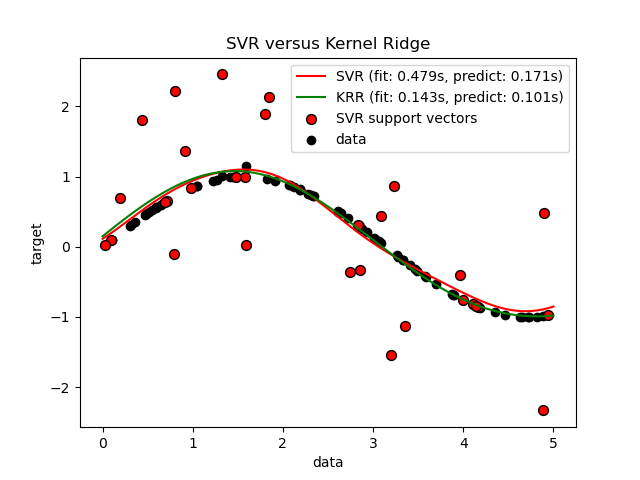
На приведенном ниже рисунке сравнивается , KernelRidge и SVR на искусственный наборе данных, который состоит из добавленной к каждым пятым синусоидальной точке данных целевой функции и сильного шума. Построена изученная модель KernelRidge и SVR, где как сложность / регуляризация, так и полоса пропускания ядра RBF были оптимизированы с помощью поиска по сетке. Изученные функции очень похожи; однако подгонка KernelRidge примерно в семь раз быстрее подбора SVR (и то, и другое с поиском по сетке). Однако прогнозирование 100000 целевых значений более чем в три раза быстрее, SVR поскольку он изучил разреженную модель, используя только примерно 1/3 из 100 обучающих точек данных в качестве опорных векторов.

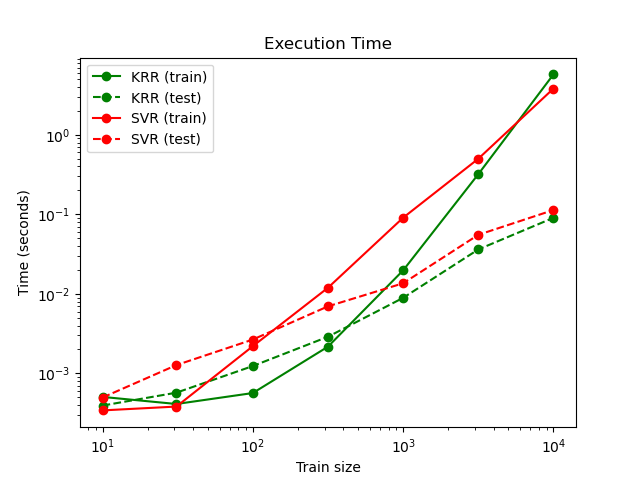
На следующем рисунке сравнивает время для подгонки и прогнозирования KernelRidge и SVR для различных размеров обучающего набора. Подгонка KernelRidge выполняется быстрее, чем SVR для обучающих выборок среднего размера (менее 1000 образцов); однако для больших тренировочных наборов SVR масштабирование лучше. Что касается времени прогнозирования, SVR это быстрее, чем KernelRidge для всех размеров обучающей выборки, из-за изученного разреженного решения. Обратите внимание, что степень разреженности и, следовательно, время прогноза зависят от параметровϵ а также $C$ из SVR; $\epsilon = 0$ соответствует плотной модели.