1.4. Метод опорных векторов SVM ¶
Метод опорных векторов (Support Vector Machines — SVM) — это набор контролируемых методов обучения, используемых для классификации , регрессии и обнаружения выбросов .
Преимущества:
- Эффективен в пространствах больших размеров.
- По-прежнему эффективен в случаях, когда количество измерений превышает количество образцов.
- Использует подмножество обучающих точек в функции принятия решений (называемых опорными векторами), поэтому это также эффективно с точки зрения памяти.
- Универсальность: для функции принятия решения могут быть указаны различные функции ядра . Предоставляются общие ядра, но также можно указать собственные ядра.
К недостаткам опорных векторных машин можно отнести:
- Если количество функций намного превышает количество выборок, избегайте чрезмерной подгонки при выборе функций ядра, и термин регуляризации имеет решающее значение.
- SVM не предоставляют напрямую оценки вероятностей, они рассчитываются с использованием дорогостоящей пятикратной перекрестной проверки (см. Оценки и вероятности ниже).
Метод опорных векторов в scikit-learn поддерживают как плотные ( numpy.ndarray и конвертируемые в это numpy.asarray), так и разреженные (любые scipy.sparse) выборочные векторы в качестве входных данных. Однако, чтобы использовать SVM для прогнозирования разреженных данных, он должен соответствовать этим данным. Для оптимальной производительности используйте C-порядковый numpy.ndarray (плотный) или scipy.sparse.csr_matrix (разреженный) с dtype=float64.
1.4.1. Классификация
SVC, NuSVC и LinearSVC являются классами, способными выполнять двоичную и мультиклассовую классификацию набора данных.
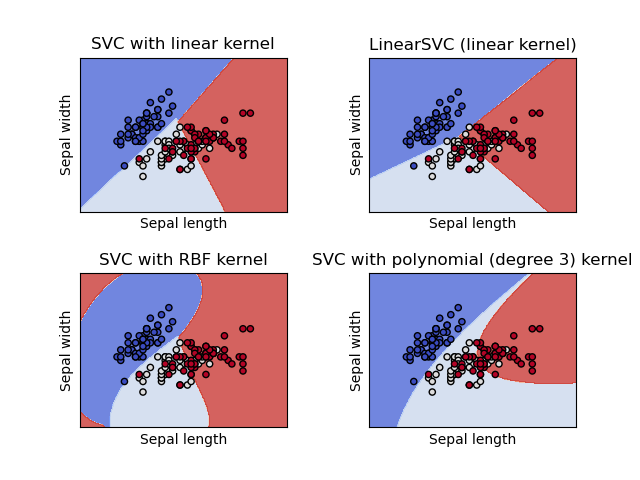
SVC и NuSVC являются аналогичными методами, но принимают несколько разные наборы параметров и имеют разные математические формулировки (см. раздел Математическая формулировка ). С другой стороны, LinearSVC это еще одна (более быстрая) реализация классификации опорных векторов для случая линейного ядра. Обратите внимание, что LinearSVC параметр не принимает kernel, так как предполагается, что он линейный. Ему также не хватает некоторых атрибутов SVC и NuSVC, например support_.
Как и другие классификаторы SVC, NuSVC и LinearSVC в качестве входных двух массивов: массив X формы (n_samples, n_features), проведение обучающих выборок, и массив y из класса меток (строки или целые числа), в форме (n_samples):
>>> from sklearn import svm >>> X = [[0, 0], [1, 1]] >>> y = [0, 1] >>> clf = svm.SVC() >>> clf.fit(X, y) SVC()
После установки модель может быть использована для прогнозирования новых значений:
>>> clf.predict([[2., 2.]]) array([1])
Функция принятия решения SVM (подробно описанная в математической формулировке ) зависит от некоторого подмножества обучающих данных, называемых опорными векторами. Некоторые свойства этих опорных векторов можно найти в атрибутах support_vectors_, support_а также n_support_:
>>> # get support vectors
>>> clf.support_vectors_
array([[0., 0.],
[1., 1.]])
>>> # get indices of support vectors
>>> clf.support_
array([0, 1]...)
>>> # get number of support vectors for each class
>>> clf.n_support_
array([1, 1]...)Примеры:
1.4.1.1. Мультиклассовая классификация
SVC и NuSVC реализовать подход «один против одного» для классификации по нескольким классам. Всего построены n_classes * (n_classes — 1) / 2 классификаторов, каждый из которых обучает данные из двух классов. Чтобы обеспечить согласованный интерфейс с другими классификаторами, опция decision_function_shape позволяет монотонно преобразовывать результаты классификаторов «один против одного» в функцию принятия решения формы «один против остальных» (n_samples, n_classes).
>>> X = [[0], [1], [2], [3]] >>> Y = [0, 1, 2, 3] >>> clf = svm.SVC(decision_function_shape='ovo') >>> clf.fit(X, Y) SVC(decision_function_shape='ovo') >>> dec = clf.decision_function([[1]]) >>> dec.shape[1] # 4 classes: 4*3/2 = 6 6 >>> clf.decision_function_shape = "ovr" >>> dec = clf.decision_function([[1]]) >>> dec.shape[1] # 4 classes 4
С другой стороны, LinearSVC реализует мультиклассовую стратегию «один против остальных», таким образом обучая n_classes модели.
>>> lin_clf = svm.LinearSVC() >>> lin_clf.fit(X, Y) LinearSVC() >>> dec = lin_clf.decision_function([[1]]) >>> dec.shape[1] 4
См. « Математическая формулировка» для полного описания решающей функции.
Обратите внимание, что LinearSVC также реализуется альтернативная мультиклассовая стратегия, так называемая мультиклассовая SVM, сформулированная Краммером и Зингером 16 , с использованием этой опции multi_class='crammer_singer'. На практике обычно предпочтительнее использовать классификацию «один против остальных», поскольку результаты в основном схожи, но время выполнения значительно меньше.
Для «один против остальных» LinearSVC атрибуты coef_ и intercept_ имеют форму (n_classes, n_features) и (n_classes, ) соответственно. Каждая строка коэффициентов соответствует одному из классификаторов n_classes «один против остальных» и аналогичных для перехватов в порядке класса «один».
В случае «один против одного» SVC и NuSVC расположение атрибутов немного сложнее. В случае линейного ядра атрибуты coef_ и intercept_ имеют форму (n_classes * (n_classes — 1) / 2, n_features) и (n_classes * (n_classes — 1) / 2) соответственно. Это похоже на схему LinearSVC, описанную выше, где каждая строка теперь соответствует двоичному классификатору. Порядок для классов от 0 до n: «0 против 1», «0 против 2»,… «0 против n», «1 против 2», «1 против 3», «1 против n»,. . . «П-1 против п».
Форма dual_coef_ является (n_classes-1, n_SV) с довольно трудно макетом обхвата. Столбцы соответствуют опорным векторам, включенным в любой из n_classes * (n_classes — 1) / 2 классификаторов «один на один». Каждый из опорных векторов используется в n_classes — 1 классификаторах. Эти n_classes — 1 записи в каждой строке соответствует двойственным коэффициентам для этих классификаторов.
Это может быть яснее на примере: рассмотрим проблему трех классов с классом 0, имеющим три опорных вектора. $v_0^0$,$v_0^1$,$v_0^2$ и классы 1 и 2, имеющие два опорных вектора $v_1^0$,$v_1^1$ а также $v_2^0$,$v_2^1$ соответственно. Для каждого опорного вектора $v_i^j$, есть два двойственных коэффициента. Назовем коэффициент опоры вектором $v_i^j$ в классификаторе между классами $i$ а также $k$ $\alpha^{j}_{i,k}$. Тогда dual_coef_ выглядит так:
| $\alpha^{0}_{0,1}$ | $\alpha^{0}_{0,2}$ | Коэффициенты для КА класса 0 |
| $\alpha^{1}_{0,1}$ | $\alpha^{1}_{0,2}$ | Коэффициенты для КА класса 0 |
| $\alpha^{2}_{0,1}$ | $\alpha^{2}_{0,2}$ | Коэффициенты для КА класса 0 |
| $\alpha^{0}_{1,0}$ | $\alpha^{0}_{1,2}$ | Коэффициенты для КА класса 1 |
| $\alpha^{1}_{1,0}$ | $\alpha^{1}_{1,2}$ | Коэффициенты для КА класса 1 |
| $\alpha^{0}_{2,0}$ | $\alpha^{0}_{2,1}$ | Коэффициенты для КА 2 класса |
| $\alpha^{1}_{2,0}$ | $\alpha^{1}_{2,1}$ | Коэффициенты для КА 2 класса |
1.4.1.2. Результаты и вероятности
Метод decision_function из SVC и NuSVC дает по классам баллов для каждого образца (или единого показателя на образец в двоичном случае). Если для параметра конструктора probability установлено значение True, включаются оценки вероятности членства в классе (из методов predict_proba и predict_log_proba). В двоичном случае вероятности калибруются с использованием шкалы Платта 9 : логистическая регрессия по оценкам SVM, согласованная с помощью дополнительной перекрестной проверки данных обучения. В случае мультикласса это расширяется в соответствии с 10 .
Примечание
Та же процедура калибровки вероятности доступна для всех оценщиков через CalibratedClassifierCV (см. Калибровка вероятности ). В случае SVC и NuSVC эта процедура встроена в libsvm, которая используется под капотом, поэтому она не полагается на scikit-learn CalibratedClassifierCV.
Перекрестная проверка, связанная с масштабированием Platt, — дорогостоящая операция для больших наборов данных. Кроме того, оценки вероятности могут не соответствовать оценкам:
- «argmax» оценок может не быть argmax вероятностей.
- в бинарной классификации образец может быть помечен
predictкак принадлежащий к положительному классу, даже если выходpredict_probaс оставляет менее 0,5; и аналогично, он может быть помечен как отрицательный, даже если выходpredict_probaбольше 0,5.
Известно также, что метод Платта имеет теоретические проблемы. Если требуются оценки достоверности, но они не обязательно должны быть вероятностями, то рекомендуется установить probability=False и использовать decision_function вместо predict_proba.
Обратите внимание, что когда decision_function_shape='ovr' и n_classes > 2, в отличие от decision_function, метод predict не пытается разорвать связи по умолчанию. Вы можете установить break_ties=True, чтобы вывод predict был таким же, как np.argmax(clf.decision_function(…), axis=1), иначе всегда будет возвращаться первый класс среди связанных классов; но имейте в виду, что это связано с вычислительными затратами. См. Пример разрыва связи SVM в примере .
1.4.1.3. Несбалансированные проблемы
В задачах, где желательно придать большее значение определенным классам или определенным отдельным образцам, можно использовать параметры class_weight и sample_weight.
SVC (но не NuSVC) реализует параметр class_weight в fit методе. Это словарь формы {class_label : value}, где значение — это число с плавающей точкой number > 0, которое устанавливает С для параметра класса class_label значение C * value. На рисунке ниже показана граница решения несбалансированной проблемы с поправкой на вес и без нее.
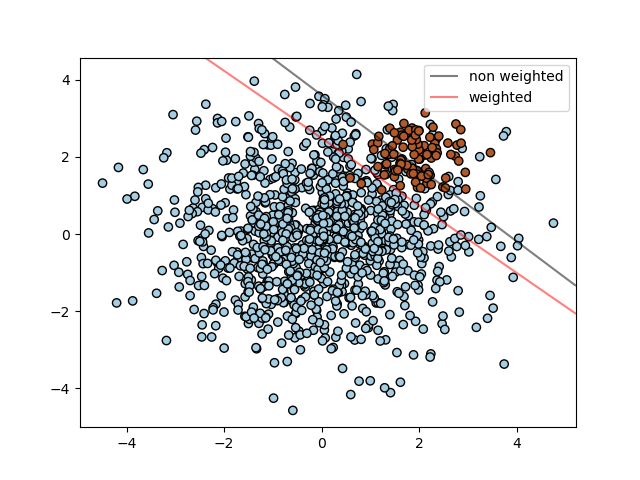
SVC, NuSVC, SVR, NuSVR, LinearSVC, LinearSVR и OneClassSVM осуществить также веса для отдельных образцов в fit методе через sample_weight параметр. Подобно тому class_weight, это устанавливает параметр C для i-го примера равным C * sample_weight[i], что побуждает классификатор правильно определять эти образцы. На рисунке ниже показано влияние взвешивания выборки на границу принятия решения. Размер кружков пропорционален весу образца:
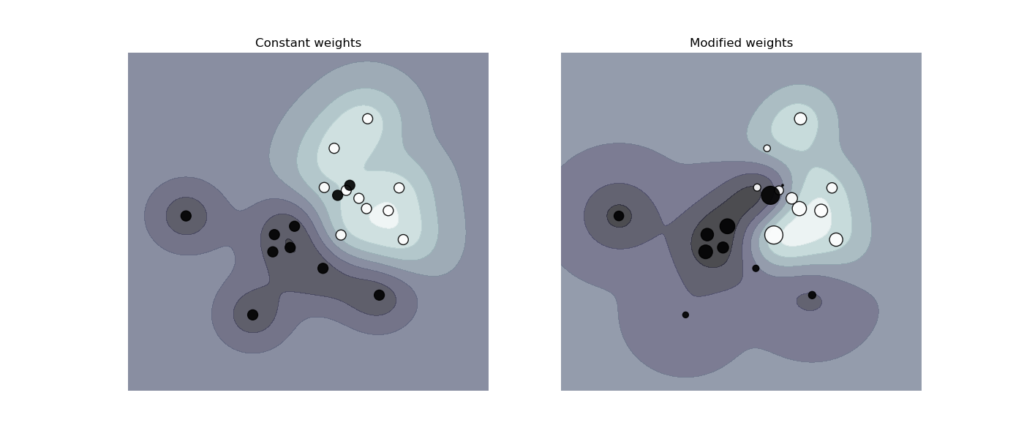
1.4.2. Регрессия
Метод классификации опорных векторов может быть расширен для решения задач регрессии. Этот метод называется регрессией опорных векторов.
Модель, созданная с помощью классификации опорных векторов (как описано выше), зависит только от подмножества обучающих данных, потому что функция затрат для построения модели не заботится о точках обучения, которые лежат за пределами поля. Аналогичным образом модель, созданная с помощью регрессии опорных векторов, зависит только от подмножества обучающих данных, поскольку функция стоимости игнорирует образцы, прогноз которых близок к их целевому значению.
Есть три различных реализаций опорных векторов регрессии: SVR, NuSVR и LinearSVR. LinearSVR обеспечивает более быструю реализацию, чем, SVR но учитывает только линейное ядро, но NuSVR реализует несколько иную формулировку, чем SVR и LinearSVR. См. Подробности реализации для получения дополнительной информации.
Как и в случае с классами классификации, метод соответствия будет принимать в качестве аргументов векторы X, y, только в этом случае ожидается, что y будет иметь значения с плавающей запятой вместо целочисленных значений:
>>> from sklearn import svm >>> X = [[0, 0], [2, 2]] >>> y = [0.5, 2.5] >>> regr = svm.SVR() >>> regr.fit(X, y) SVR() >>> regr.predict([[1, 1]]) array([1.5])
1.4.3. Оценка плотности, обнаружение новизны
Класс OneClassSVM реализует одноклассную SVM, которая используется для обнаружения выбросов.
См. Раздел Обнаружение новинок и выбросов для описания и использования OneClassSVM.
1.4.4. Сложность
Машины опорных векторов — мощные инструменты, но их требования к вычислениям и хранению быстро растут с увеличением числа обучающих векторов. Ядром SVM является задача квадратичного программирования (QP), отделяющая опорные векторы от остальной части обучающих данных. Решатель QP, используемый реализацией на основе libsvm, масштабируется между $O(n_{features} \times n_{samples}^2)$ а также $O(n_{features} \times n_{samples}^3)$ в зависимости от того, насколько эффективно используется кеш libsvm на практике (зависит от набора данных). Если данные очень скудныеnfeatures следует заменить на среднее количество ненулевых функций в векторной выборке.
Для линейного случая, алгоритм , используемый в LinearSVC по liblinear реализации является гораздо более эффективным , чем его libsvm SVC аналог и может масштабироваться почти линейно миллионы образцов и/или функций.
1.4.5. Советы по практическому использованию
- Избегая копирования данных : Для
SVC,SVR,NuSVCиNuSVRесли данные , передаваемые в некоторых методов не C упорядоченный непрерывный и двойной точности, то он будет скопирован перед вызовом основной реализации C. Вы можете проверить, является ли данный массив numpy непрерывным, проверив егоflagsатрибут.
ForLinearSVC(иLogisticRegression) любой ввод, переданный как массив numpy, будет скопирован и преобразован в liblinear внутреннее разреженное представление данных (числа с плавающей запятой двойной точности и индексы int32 ненулевых компонентов). Если вы хотите вписать крупномасштабный линейный классификатор без копирования плотного numpy C-смежного массива двойной точности в качестве входных данных, мы предлагаемSGDClassifierвместо этого использовать этот класс. Целевая функция может быть настроена почти так же, какLinearSVCмодель. - Ядро Размер кэша: Для
SVC,SVR,NuSVCиNuSVR, размера кэша ядра оказывает сильное влияние на время наработки на более серьезные проблемы. Если у вас достаточно оперативной памяти, рекомендуется установитьcache_sizeболее высокое значение, чем значение по умолчанию 200 (МБ), например 500 (МБ) или 1000 (МБ). - Настройка C :
Cэто1по умолчанию , и это разумный выбор по умолчанию. Если у вас много зашумленных наблюдений, вам следует уменьшить его: уменьшение C соответствует большей регуляризации.LinearSVCиLinearSVRменее чувствительны к тому,Cкогда он становится большим, а результаты прогнозирования перестают улучшаться после определенного порога. Между тем, большиеCзначения потребуют больше времени для обучения, иногда до 10 раз дольше, как показано на рисунке 11. - Алгоритмы машины опорных векторов не масштабируются, поэтому настоятельно рекомендуется масштабировать данные . Например, масштабируйте каждый атрибут во входном векторе X до [0,1] или [-1, + 1] или стандартизируйте его, чтобы он имел среднее значение 0 и дисперсию 1. Обратите внимание, что такое же масштабирование должно быть применено к проверочному вектору, чтобы получить значимые результаты. Это легко сделать с помощью
Pipeline:
>>> from sklearn.pipeline import make_pipeline >>> from sklearn.preprocessing import StandardScaler >>> from sklearn.svm import SVC >>> clf = make_pipeline(StandardScaler(), SVC())
См. Раздел « Предварительная обработка данных» для получения более подробной информации о масштабировании и нормализации.
- Что касается
shrinkingпараметра, цитируя 12 : мы обнаружили, что если количество итераций велико, то сжатие может сократить время обучения. Однако, если мы решим проблему оптимизации слабо (например, используя большой допуск остановки), код без использования сжатия может быть намного быстрее. - Параметр
nuвNuSVC/OneClassSVM/NuSVRприближает долю ошибок обучения и опорных векторов. - В
SVCслучае, если данные несбалансированы (например, много положительных и мало отрицательных), установитеclass_weight='balanced'и/или попробуйте разные параметры штрафаC. - Случайность базовых реализаций : базовые реализации
SVCиNuSVCиспользуют генератор случайных чисел только для перетасовки данных для оценки вероятности (когдаprobabilityустановлено значениеTrue). Этой случайностью можно управлять с помощьюrandom_stateпараметра. Еслиprobabilityустановлено значение,Falseэти оценки не являются случайными иrandom_stateне влияют на результаты. БазоваяOneClassSVMреализация аналогична реализациямSVCиNuSVC. Поскольку оценка вероятности не предусмотренаOneClassSVM, она не является случайной.
БазоваяLinearSVCреализация использует генератор случайных чисел для выбора функций при подгонке модели с двойным координатным спуском (т. е. Когдаdualустановлено значениеTrue). Таким образом, нередки случаи, когда для одних и тех же входных данных получаются несколько разные результаты. Если это произойдет, попробуйте использовать меньшийtolпараметр. Этой случайностью также можно управлять с помощьюrandom_stateпараметра. Когдаdualустановлено дляFalseбазовой реализации,LinearSVCне является случайным иrandom_stateне влияет на результаты. - Использование штрафных санкций L1, как предусмотрено в LinearSVC(penalty=’l1′, dual=False), дает разреженное решение, т.е. только подмножество весов признаков отличается от нуля и вносит вклад в функцию принятия решения. Увеличение C дает более сложную модель (выбирается больше функций). Значение C, которое дает модель «нулевой» (все веса равны нулю) может быть вычислено с использованием
l1_min_c.
1.4.6. Функции ядра
Функция ядра может быть любой из следующих:
- линейный: $\langle x, x’\rangle$.
- полином: $(\gamma \langle x, x’\rangle + r)^d$, где dуказывается параметром
degree, $r$ поcoef0. - rbf: $\exp(-\gamma |x-x’|^2)$, где $\gamma$ указывается параметром
gamma, должно быть больше 0. - сигмовидный $\tanh(\gamma \langle x,x’\rangle + r)$, где $r$ указывается
coef0.
Разные ядра задаются kernel параметром:
>>> linear_svc = svm.SVC(kernel='linear') >>> linear_svc.kernel 'linear' >>> rbf_svc = svm.SVC(kernel='rbf') >>> rbf_svc.kernel 'rbf'
1.4.6.1. Параметры ядра RBF
При обучении SVM с ядром Радиальной Базовой Функции (Radial Basis Function — RBF) необходимо учитывать два параметра: C и gamma. Параметр C, общий для всех ядер SVM, компенсирует неправильную классификацию обучающих примеров простотой поверхности принятия решений. Низкое значение C делает поверхность принятия решения гладкой, а высокое C правильные классификации всех обучающих примеров. gamma определяет, какое влияние имеет один обучающий пример. Чем больше gamma, тем ближе другие примеры должны быть затронуты.
Правильный выбор C и gamma имеет решающее значение для производительности SVM. Рекомендуется использовать GridSearchCV с C и gamma экспоненциально далеко друг от друга, чтобы выбрать хорошие значения.
Примеры:
1.4.6.2. Пользовательские ядра
Вы можете определить свои собственные ядра, указав ядро как функцию Python или предварительно вычислив матрицу Грама.
Классификаторы с пользовательскими ядрами ведут себя так же, как и любые другие классификаторы, за исключением того, что:
- Поле
support_vectors_теперь пустое, в нем хранятся только индексы опорных векторовsupport_ - Ссылка (а не копия) первого аргумента
fit()метода сохраняется для использования в будущем. Если этот массив изменится между использованиемfit()иpredict()вы получите неожиданные результаты.
1.4.6.2.1. Использование функций Python в качестве ядер
Вы можете использовать собственные определенные ядра, передав функцию kernel параметру.
Ваше ядро должно принимать в качестве аргументов две матрицы формы (n_samples_1, n_features), (n_samples_2, n_features) и возвращает матрицу ядра в форме (n_samples_1, n_samples_2)
Следующий код определяет линейное ядро и создает экземпляр классификатора, который будет использовать это ядро:
>>> import numpy as np >>> from sklearn import svm >>> def my_kernel(X, Y): ... return np.dot(X, Y.T) ... >>> clf = svm.SVC(kernel=my_kernel)
Примеры:
1.4.6.2.2. Используя матрицу Грама
Вы можете передать предварительно вычисленные ядра, используя kernel='precomputed' параметр. Затем вы должны передать матрицу Грама вместо X к fit и predict методам. Должны быть предоставлены значения ядра между всеми обучающими векторами и тестовыми векторами:
>>> import numpy as np >>> from sklearn.datasets import make_classification >>> from sklearn.model_selection import train_test_split >>> from sklearn import svm >>> X, y = make_classification(n_samples=10, random_state=0) >>> X_train , X_test , y_train, y_test = train_test_split(X, y, random_state=0) >>> clf = svm.SVC(kernel='precomputed') >>> # linear kernel computation >>> gram_train = np.dot(X_train, X_train.T) >>> clf.fit(gram_train, y_train) SVC(kernel='precomputed') >>> # predict on training examples >>> gram_test = np.dot(X_test, X_train.T) >>> clf.predict(gram_test) array([0, 1, 0])
1.4.7. Математическая постановка
Машина опорных векторов конструирует гиперплоскость или набор гиперплоскостей в пространстве большой или бесконечной размерности, которые можно использовать для классификации, регрессии или других задач. Интуитивно хорошее разделение достигается за счет гиперплоскости, которая имеет наибольшее расстояние до ближайших точек обучающих данных любого класса (так называемый функциональный запас), поскольку, как правило, чем больше запас, тем ниже ошибка обобщения классификатора. На рисунке ниже показана функция решения для линейно разделяемой задачи с тремя образцами на границах запаса, называемыми «векторами поддержки»:

В общем, когда проблема не является линейно разделимой, опорные векторы являются выборками в пределах границ поля.
Мы рекомендуем 13 и 14 как хорошие справочные материалы по теории и практике SVM.
1.4.7.1. SVC
Данные обучающие векторы $x_i \in \mathbb{R}^p$, i = 1,…, n, в двух классах, и вектор $y \in \left\{1, -1\right\}^n$ наша цель найти $w \in\mathbb{R}^p$ а также $b \in \mathbb{R}$ такой, что предсказание, данное $\text{sign} (w^T\phi(x) + b)$ подходит для большинства образцов.
SVC решает следующую основную проблему:
$$\min_ {w, b, \zeta} \frac{1}{2} w^T w + C \sum_{i=1}^{n} \zeta_i$$
$$\textrm {subject to } y_i (w^T \phi (x_i) + b) \geq 1 — \zeta_i,$$
$$\zeta_i \geq 0, i=1, …, n$$
Интуитивно мы пытаемся максимизировать маржу (минимизируя $||w||^2 = w^Tw$), при этом налагается штраф, если образец неправильно классифицирован или находится в пределах границ маржи. В идеале значение $y_i(w^T \phi (x_i) + b)$ было бы $\geq 1$ для всех образцов, что указывает на идеальный прогноз. Но обычно проблемы не всегда можно идеально отделить с помощью гиперплоскости, поэтому мы позволяем некоторым образцам находиться на расстоянии $\zeta_i$ от их правильной границы поля. Срок штрафа C контролирует силу этого штрафа и, как результат, действует как параметр обратной регуляризации (см. Примечание ниже).
Двойственная проблема первобытного:
$$\min_{\alpha} \frac{1}{2} \alpha^T Q \alpha — e^T \alpha$$
$$\textrm {subject to } y^T \alpha = 0$$
$$0 \leq \alpha_i \leq C, i=1, …, n$$
где e вектор всех единиц, а $Q$ является n от n положительно полуопределенная матрица, $Q_{ij} \equiv y_i y_j K(x_i, x_j)$, где $K(x_i, x_j) = \phi (x_i)^T \phi (x_j)$ это ядро. Условияαi называются двойственными коэффициентами, и они ограничены сверху величиной $C$. Это двойное представление подчеркивает тот факт, что обучающие векторы неявно отображаются в более высокое (возможно, бесконечное) пространство с помощью функции $\phi$: см. трюк с ядром .
Как только проблема оптимизации решена, выходные данные функции решения для данной выборкиx становится:
$$\sum_{i\in SV} y_i \alpha_i K(x_i, x) + b,$$
и предсказанный класс соответствуют его знаку. Нам нужно только просуммировать по опорным векторам (то есть выборкам, которые лежат в пределах поля), потому что двойные коэффициенты $\alpha_i$ равны нулю для остальных образцов.
Доступ к этим параметрам можно получить через атрибуты, dual_coef_ содержащие продукт.yiαi, support_vectors_ который содержит опорные векторы и intercept_ независимый член $b$
Примечание
В то время как модели SVM, полученные из libsvm и liblinear, используют в C качестве параметра регуляризации, большинство других оценщиков используют alpha. Точная эквивалентность между степенью регуляризации двух моделей зависит от точной целевой функции, оптимизированной моделью. Например, когда используется оценка Ridge регрессии, связь между ними задается как $C = \frac{1}{alpha}$
1.4.7.2. LinearSVC
Первичную задачу можно эквивалентно сформулировать как
$$\min_ {w, b} \frac{1}{2} w^T w + C \sum_{i=1}\max(0, y_i (w^T \phi(x_i) + b)),$$
где мы используем потерю шарнира . Это форма, которая напрямую оптимизируется LinearSVC, но, в отличие от двойной формы, она не включает внутренние продукты между семплами, поэтому знаменитый трюк с ядром не может быть применен. Вот почему только линейное ядро поддерживается LinearSVC ($\phi$ — тождественная функция).
1.4.7.3. NuSVC
В ν-SVC рецептура 15 представляет собой повторную параметризацию $C$-SVC и, следовательно, математически эквивалентен.
Мы вводим новый параметр $\nu$ (вместо $C$), который контролирует количество опорных векторов и маржинальных ошибок :$\nu \in (0, 1]$ — это верхняя граница доли маржинальных ошибок и нижняя граница доли опорных векторов. Погрешность маржи соответствует образцу, лежащему не на той стороне границы маржи: она либо неправильно классифицирована, либо классифицирована правильно, но не выходит за пределы маржи.
1.4.7.4. SVR
Данные обучающие векторы $x_i \in \mathbb{R}^p$, i = 1,…, n, и вектор $y \in \mathbb{R}^n$ $\varepsilon$-SVR решает следующую основную проблему:
$$\min_ {w, b, \zeta, \zeta^*} \frac{1}{2} w^T w + C \sum_{i=1}^{n} (\zeta_i + \zeta_i^*)$$
$$\textrm {subject to } y_i — w^T \phi (x_i) — b \leq \varepsilon + \zeta_i,$$
$$w^T \phi (x_i) + b — y_i \leq \varepsilon + \zeta_i^*,$$
$$\zeta_i, \zeta_i^* \geq 0, i=1, …, n$$
Здесь мы штрафуем образцы, прогноз которых не ниже εподальше от их истинной цели. Эти образцы штрафуют цель на $\zeta_i$ или $\zeta_i^*$, в зависимости от того, лежат ли их прогнозы выше или ниже $\varepsilon$ диапазона.
Двойная проблема:
$$\min_{\alpha, \alpha^*} \frac{1}{2} (\alpha — \alpha^*)^T Q (\alpha — \alpha^*) + \varepsilon e^T (\alpha + \alpha^*) — y^T (\alpha — \alpha^*)$$
$$\textrm {subject to } e^T (\alpha — \alpha^*) = 0$$
$$0 \leq \alpha_i, \alpha_i^* \leq C, i=1, …, n$$
где $e$ вектор всех единиц, $Q$ является $n$ от $n$ положительно полуопределенная матрица, $Q_{ij} \equiv K(x_i, x_j) = \phi (x_i)^T \phi (x_j)$ это ядро. Здесь обучающие векторы неявно отображаются в более высокое (возможно, бесконечное) пространство с помощью функции $\phi$.
Прогноз такой:
$$\sum_{i \in SV}(\alpha_i — \alpha_i^*) K(x_i, x) + b$$
К этим параметрам можно получить доступ через атрибуты, dual_coef_ которые содержат разницу $\alpha_i — \alpha_i^*$ , support_vectors_ который содержит опорные векторы и intercept_ независимый член
1.4.7.5. LinearSVR
Первичную задачу можно эквивалентно сформулировать как
$$\min_ {w, b} \frac{1}{2} w^T w + C \sum_{i=1}\max(0, |y_i — (w^T \phi(x_i) + b)| — \varepsilon),$$
где мы используем нечувствительные к эпсилону потери, т. е. ошибки менее $\varepsilon$ игнорируются. Это форма, которая напрямую оптимизируется LinearSVR.
1.4.8. Детали реализации
Внутри мы используем libsvm 12 и liblinear 11 для обработки всех вычислений. Эти библиотеки обернуты с использованием C и Cython. Описание реализации и детали используемых алгоритмов см. В соответствующих документах.
Рекомендации:
- Платт «Вероятностные выходы для SVM и сравнения с регуляризованными методами правдоподобия» .
- Ву, Линь и Вен, «Оценки вероятности для классификации нескольких классов путем попарного связывания» , JMLR 5: 975-1005, 2004.
- Фан, Ронг-Эн и др., «LIBLINEAR: библиотека для большой линейной классификации». , Журнал исследований машинного обучения 9. августа (2008): 1871-1874.
- Чанг и Лин, LIBSVM: библиотека для машин опорных векторов .
- Епископ, Распознавание образов и машинное обучение , глава 7 Машины с разреженным ядром
- «Учебное пособие по регрессии опорных векторов » , Алекс Дж. Смола, Бернхард Шёлкопф — Архив статистики и вычислений Том 14, выпуск 3, август 2004 г., с. 199-222.
- Schölkopf et. al Новые алгоритмы опорных векторов
- Краммер и Зингер об алгоритмической реализации векторных машин на основе многоклассового ядра , JMLR 2001.
