1.5. Стохастический градиентный спуск ¶

Стохастический градиентный спуск (SGD) — это простой, но очень эффективный подход к подгонке линейных классификаторов и регрессоров под выпуклые функции потерь, такие как (линейные) Метод опорных векторов и логистическая регрессия . Несмотря на то, что SGD существует в сообществе машинного обучения уже давно, совсем недавно он привлек значительное внимание в контексте крупномасштабного обучения.

SGD успешно применяется для решения крупномасштабных и разреженных задач машинного обучения, часто встречающихся при классификации текста и обработке естественного языка. Учитывая, что данные немногочисленны, классификаторы в этом модуле легко масштабируются для решения задач с более чем $10^5$ обучающими примерами и более чем $10^5$ функциями.

Строго говоря, SGD — это просто метод оптимизации и не соответствует конкретному семейству моделей машинного обучения. Это всего лишь способ обучить модель. Часто экземпляр SGDClassifier или SGDRegressor будет иметь эквивалентный оценщик в scikit-learn API, потенциально используя другой метод оптимизации. Например, использование SGDClassifier(loss='log') результатов в логистической регрессии, т. Е. Модель, эквивалент LogisticRegression которой подбирается через SGD, а не подгоняется одним из других решателей в LogisticRegression. Точно так же SGDRegressor(loss=’squared_loss’, penalty=’l2′) и Ridge решают одну и ту же задачу оптимизации разными способами.

Преимущества стохастического градиентного спуска:

• Эффективность.
• Простота реализации (множество возможностей для настройки кода).

К недостаткам стохастического градиентного спуска можно отнести:

• SGD требует ряда гиперпараметров, таких как параметр регуляризации и количество итераций.
• SGD чувствителен к масштабированию функций.

1.5.1. Классификация

Класс SGDClassifier реализует простую процедуру обучения стохастическим градиентным спуском, которая поддерживает различные функции потерь и штрафы за классификацию. Ниже приведена граница принятия решения SGDClassifier обученного с потерей шарнира, эквивалентного линейному SVM.

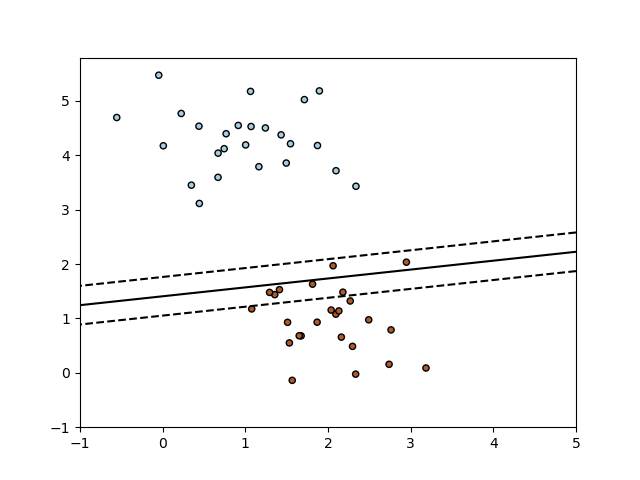
Как и другие классификаторы, SGD должен быть оснащен двумя массивами: массивом X формы (n_samples, n_features), содержащим обучающие образцы, и массивом формы y (n_samples,), содержащим целевые значения (метки классов) для обучающих образцов:

>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
>>> clf.fit(X, y)
SGDClassifier(max_iter=5)

После установки модель может быть использована для прогнозирования новых значений:

>>> clf.predict([[2., 2.]])
array([1])

SGD подгоняет линейную модель к обучающим данным. Атрибут coef_ содержит параметры модели:

>>> clf.coef_
array([[9.9..., 9.9...]])

Атрибут intercept_ содержит перехват (ака смещение или смещение):

>>> clf.intercept_
array([-9.9...])

Параметр определяет, должна ли модель использовать точку пересечения, т. Е. Смещенную гиперплоскость fit_intercept.

Расстояние со знаком до гиперплоскости (вычисленное как скалярное произведение между коэффициентами и входной выборкой плюс точка пересечения) определяется как SGDClassifier.decision_function:

>>> clf.decision_function([[2., 2.]])
array([29.6...])

Конкретную функцию потерь можно установить с помощью loss параметра.  SGDClassifier поддерживает следующие функции потерь:

• loss="hinge": (soft-margin) линейная машина опорных векторов,
• loss="modified_huber": сглаженная потеря петель,
• loss="log": логистическая регрессия,
• и все потери регрессии ниже. В этом случае цель кодируется как -1 или 1, и проблема рассматривается как проблема регрессии. Предсказанный класс тогда соответствует знаку прогнозируемой цели.

Пожалуйста, обратитесь к математическому разделу ниже для формул. Первые две функции потерь являются ленивыми, они обновляют параметры модели только в том случае, если пример нарушает маржинальное ограничение, что делает обучение очень эффективным и может привести к более разреженным моделям (то есть с большим количеством нулевых коэффициентов), даже когда используется штраф L2.

Использование loss="log" или loss="modified_huber" включает predict_proba метод, который дает вектор оценок вероятности $P (y|x)$ за образец $x$:

>>> clf = SGDClassifier(loss="log", max_iter=5).fit(X, y)
>>> clf.predict_proba([[1., 1.]])
array([[0.00..., 0.99...]])

Конкретный штраф можно установить с помощью penalty параметра. SGD поддерживает следующие штрафы:

• penalty="l2": L2 Норма штрафа вкл coef_.
• penalty="l1": Штраф нормы L1 включен coef_.
• penalty="elasticnet": Выпуклая комбинация L2 и L1; (1 - l1_ratio) * L2 + l1_ratio * L1

По умолчанию установлено penalty="l2". Штраф L1 приводит к разреженным решениям, сводя большинство коэффициентов к нулю. Elastic Net 11  устраняет некоторые недостатки штрафа L1 при наличии сильно коррелированных атрибутов. Параметр l1_ratioуправляет выпуклой комбинацией штрафов L1 и L2.

SGDClassifier поддерживает многоклассовую классификацию путем объединения нескольких двоичных классификаторов по схеме «один против всех» (OVA). Для каждого из $K$ классов, изучается двоичный классификатор, который отличает этот классификатор от всех остальных $K−1$ классы. Во время тестирования мы вычисляем показатель достоверности (т. е. Подписанные расстояния до гиперплоскости) для каждого классификатора и выбираем класс с наибольшей достоверностью. На рисунке ниже показан подход OVA к набору данных радужной оболочки глаза. Пунктирные линии представляют три классификатора OVA; цвета фона показывают поверхность принятия решения, вызванную тремя классификаторами.

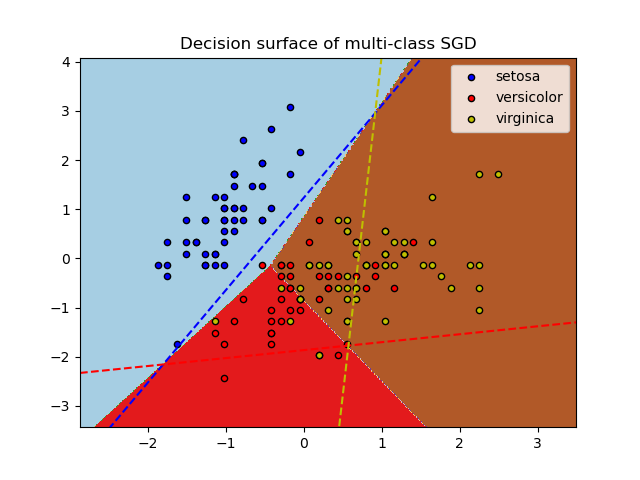
В случае мультиклассовой классификации coef_это двумерный массив формы (n_classes, n_features) и intercept_одномерный массив формы (n_classes,). I-я строка coef_ содержит весовой вектор классификатора OVA для i-го класса; классы индексируются в порядке возрастания (см. атрибут classes_). Обратите внимание, что, в принципе, они позволяют создать вероятностную модель loss="log"и loss="modified_huber" больше подходят для классификации «один против всех».

SGDClassifier поддерживает как взвешенные классы, так и взвешенные экземпляры через параметры соответствия class_weightи sample_weight. См. Примеры ниже и строку документации SGDClassifier.fit для получения дополнительной информации.

SGDClassifier поддерживает усредненный SGD (ASGD) 10 . Усреднение можно включить настройкой average=True. ASGD выполняет те же обновления, что и обычный SGD (см. Математическая формулировка ), но вместо использования последнего значения коэффициентов в качестве coef_ атрибута (т.е. значений последнего обновления) coef_вместо этого устанавливается среднее значение коэффициентов по всем параметрам. обновления. То же самое и с intercept_ атрибутом. При использовании ASGD скорость обучения может быть больше и даже постоянной, что приводит к сокращению времени обучения на некоторых наборах данных.

Для классификации с логистическими потерями доступен другой вариант SGD со стратегией усреднения с алгоритмом стохастического среднего градиента (SAG), доступным в качестве решателя в LogisticRegression.

1.5.2. Регрессия

Класс SGDRegressor реализует простую процедуру обучения стохастическим градиентным спуском, которая поддерживает различные функции потерь и штрафы для соответствия моделям линейной регрессии. SGDRegressor хорошо подходят для задач регрессии с большим количеством учебных образцов (> 10.000), для других проблем , которые мы рекомендуем Ridge, Lasso или ElasticNet.

Конкретную функцию потерь можно установить с помощью loss параметра. SGDRegressor поддерживает следующие функции потерь:

• loss="squared_loss": Обыкновенный метод наименьших квадратов,
• loss="huber": Потеря Хубера для надежной регрессии,
• loss="epsilon_insensitive": линейная регрессия опорных векторов.

Пожалуйста, обратитесь к математическому разделу ниже для формул. Функции потерь, нечувствительные к Хуберу и эпсилону, могут использоваться для надежной регрессии. Ширина нечувствительной области должна быть указана с помощью параметра epsilon. Этот параметр зависит от масштаба целевых переменных.

penaltyПараметр определяет регуляризации , который должен использоваться (смотри описание выше в разделе классификации).

SGDRegressor также поддерживает среднюю ставку SGD 10 (и здесь снова см. описание выше в разделе классификации).

Для регрессии с квадратом потерь и штрафом l2 доступен другой вариант SGD со стратегией усреднения с алгоритмом стохастического среднего градиента (SAG), доступным в качестве решателя в Ridge.

1.5.3. Стохастический градиентный спуск для разреженных данных

Имеется встроенная поддержка разреженных данных, представленных в любой матрице в формате, поддерживаемом scipy.sparse . Однако для максимальной эффективности используйте формат матрицы CSR, как определено в scipy.sparse.csr_matrix .

1.5.4. Сложность

Основным преимуществом SGD является его эффективность, которая в основном линейна по количеству обучающих примеров. Если $X$ — матрица размера $(n, p)$, обучение стоит $O(k n \bar p)$, где $k$ — количество итераций (эпох), а $\bar p$ — среднее количество ненулевых атрибутов в выборке.

Однако недавние теоретические результаты показывают, что время выполнения для получения желаемой точности оптимизации не увеличивается с увеличением размера обучающей выборки.

1.5.5. Критерий остановки

Классы SGDClassifier и SGDRegressor предоставляют два критерия для остановки алгоритма при достижении заданного уровня сходимости:

• С early_stopping=True помощью входные данные разделяются на обучающий набор и набор проверки. Затем модель настраивается на обучающий набор, и критерий остановки основан на оценке прогноза (с использованием scoreметода), вычисленной на проверочном наборе. Размер набора проверки можно изменить с помощью параметра validation_fraction.
• При early_stopping=False этом модель подбирается для всех входных данных, а критерий остановки основан на целевой функции, вычисленной на обучающих данных.

В обоих случаях критерий оценивается один раз за эпоху, и алгоритм останавливается, когда критерий не улучшает n_iter_no_change раз подряд. Улучшение оценивается с абсолютным допуском tol, и алгоритм останавливается в любом случае после максимального количества итераций max_iter.

1.5.6. Советы по практическому использованию

• Стохастический градиентный спуск чувствителен к масштабированию функций, поэтому настоятельно рекомендуется масштабировать ваши данные. Например, масштабируйте каждый атрибут во входном векторе $X$ до [0,1] или [-1, + 1] или стандартизируйте его так, чтобы он имел среднее значение 0 и дисперсию 1. Обратите внимание, что такое же масштабирование должно быть применено к проверочному вектору, чтобы получить значимые результаты. Это легко сделать с помощью StandardScaler:

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)  # Don't cheat - fit only on training data
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)  # apply same transformation to test data

# Or better yet: use a pipeline!
from sklearn.pipeline import make_pipeline
est = make_pipeline(StandardScaler(), SGDClassifier())
est.fit(X_train)
est.predict(X_test)

Если ваши атрибуты имеют внутреннюю шкалу (например, частота слов или особенности индикатора), масштабирование не требуется.

• Нахождение разумного условия регуляризации αлучше всего выполнять с помощью автоматического поиска по гиперпараметрам, например, GridSearchCV или RandomizedSearchCV, как правило, в диапазоне 10.0**-np.arange(1,7).
• Эмпирическим путем мы обнаружили, что SGD сходится после наблюдения примерно 10 ^ 6 обучающих выборок. Таким образом, разумное первое предположение о количестве итераций: где n — размер обучающего набора max_iter = np.ceil(10**6 / n)
• Если вы примените SGD к функциям, извлеченным с помощью PCA, мы обнаружили, что часто бывает разумно масштабировать значения функций некоторой константой c, чтобы средняя норма L2 обучающих данных была равна единице.
• Мы обнаружили, что Averaged SGD лучше всего работает с большим количеством функций и более высоким eta0.

1.5.7. Математическая постановка

Мы описываем здесь математические детали процедуры SGD. Хороший обзор показателей сходимости можно найти в 12 .

Учитывая набор обучающих примеров $(x_1,y_1),…,(x_n,y_n)$ где $x_i \in R^m$ а также $y_i \in R$ ($y_i \in−1,1$ для классификации), наша цель — изучить линейную функцию оценки $f(x) = w^T x + b$ с параметрами модели $w \in R^m$ и перехватить $b \in R$. Чтобы делать прогнозы для бинарной классификации, мы просто смотрим на знак $f(x)$. Чтобы найти параметры модели, мы минимизируем регуляризованную ошибку обучения, определяемую выражением
$$E(w,b) = \frac{1}{n}\sum_{i=1}^{n} L(y_i, f(x_i)) + \alpha R(w)$$

где L является функцией потерь, которая измеряет соответствие модели и R — термин регуляризации (также известный как штраф), который снижает сложность модели; α>0 — неотрицательный гиперпараметр, контролирующий степень регуляризации.

Различные варианты для $L$ влекут за собой разные классификаторы или регрессоры:

• Шарнир (мягкий край): эквивалент классификации опорных векторов $L(y_i, f(x_i)) = \max(0, 1 — y_i f(x_i))$.
• Персептрон: $L(y_i, f(x_i)) = \max(0, — y_i f(x_i))$.
• Модифицированный Хубер: $L(y_i, f(x_i)) = \max(0, — y_i f(x_i))$ если $y_i f(x_i) >1$, иначе $L(y_i, f(x_i)) = -4 y_i f(x_i)$.
• Log: эквивалент логистической регрессии. $L(y_i, f(x_i)) = \log(1 + \exp (-y_i f(x_i)))$
• Метод наименьших квадратов: линейная регрессия (гребень или лассо в зависимости от $R$) $L(y_i, f(x_i)) = \frac{1}{2}(y_i — f(x_i))^2$
• Хубер: менее чувствителен к выбросам, чем метод наименьших квадратов. Это эквивалентно наименьшим квадратам, когда $|y_i — f(x_i)| \leq \varepsilon$, иначе $L(y_i, f(x_i)) = \varepsilon |y_i — f(x_i)| — \frac{1}{2}\varepsilon^2$.
• Нечувствительность к эпсилону: (soft-margin) эквивалент регрессии опорных векторов $L(y_i, f(x_i)) = \max(0, |y_i — f(x_i)| — \varepsilon)$. 

Все приведенные выше функции потерь можно рассматривать как верхнюю границу ошибки неправильной классификации (потери ноль-единица), как показано на рисунке ниже.

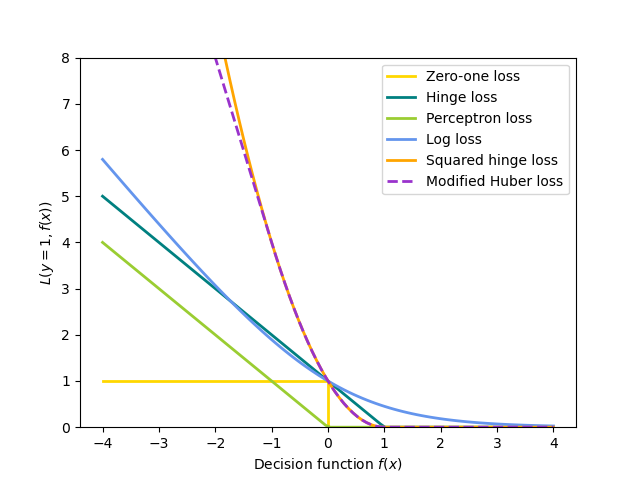
Популярные варианты срока регуляризации $R$ ( penalty параметр) включают:

• Норма L2: $R(w) := \frac{1}{2} \sum_{j=1}^{m} w_j^2 = ||w||_2^2$
• L1 норма: $R(w) := \sum_{j=1}^{m} |w_j|$, что приводит к разреженным решениям.
• Эластичная сетка: $R(w) := \frac{\rho}{2} \sum_{j=1}^{n} w_j^2 +(1-\rho) \sum_{j=1}^{m} |w_j|$, выпуклая комбинация L2 и L1, где $\rho$ дается 1 - l1_ratio

На рисунке ниже показаны контуры различных членов регуляризации в двумерном пространстве параметров ($m=2$) когда $R(w) = 1$.

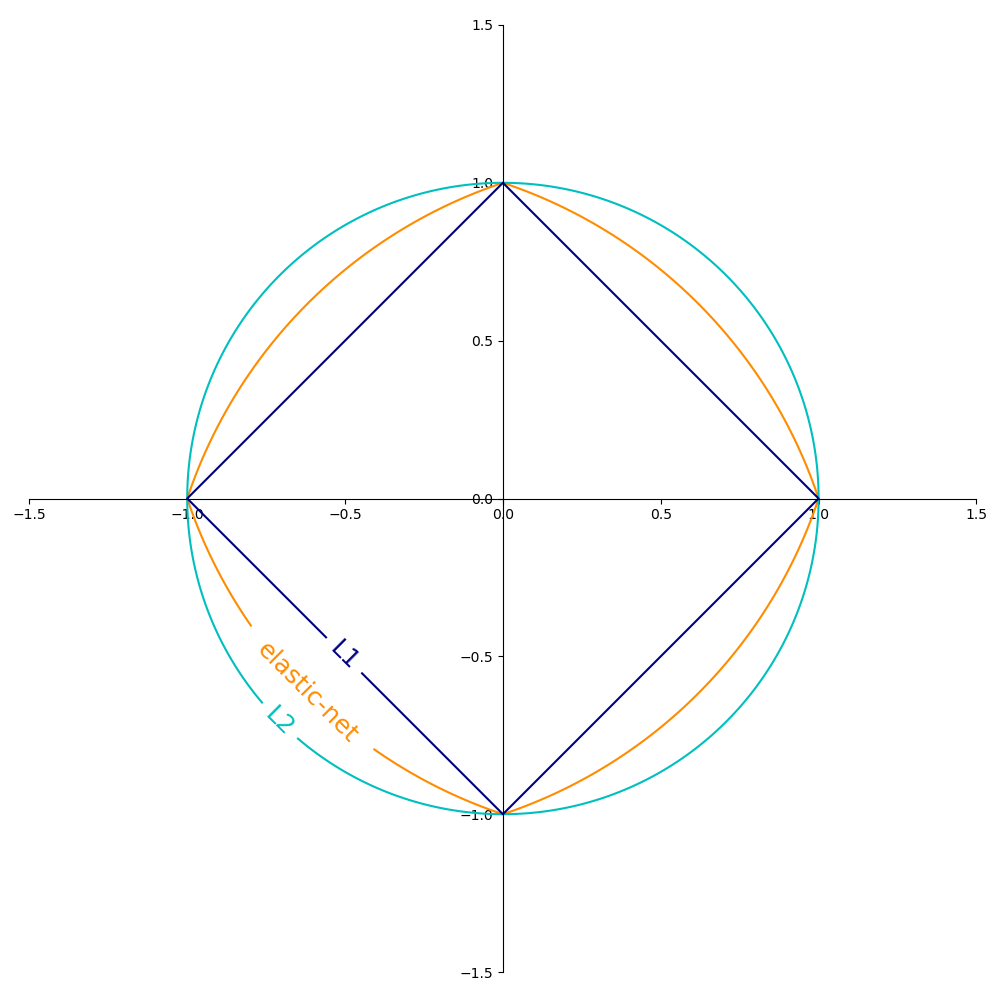
1.5.7.1. SGD

Стохастический градиентный спуск — это метод оптимизации для задач безусловной оптимизации. В отличие от (пакетного) градиентного спуска, SGD аппроксимирует истинный градиент $E(w,b)$ рассматривая один обучающий пример за раз.

Класс SGDClassifier реализует процедуру обучения SGD первого порядка. Алгоритм повторяет обучающие примеры и для каждого примера обновляет параметры модели в соответствии с правилом обновления, заданным
$$w \leftarrow w — \eta \left[\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial L(w^T x_i + b, y_i)}{\partial w}\right]$$

где η- это скорость обучения, которая контролирует размер шага в пространстве параметров. Перехватbобновляется аналогично, но без регуляризации (и с дополнительным распадом для разреженных матриц, как подробно описано в деталях реализации ).

Скорость обучения ηможет быть как постоянным, так и постепенно затухающим. Для классификации расписание скорости обучения по умолчанию ( learning_rate='optimal') задается следующим образом:
$$\eta^{(t)} = \frac {1}{\alpha (t_0 + t)}$$

где $t$ шаг по времени (всего шагов по времени n_samples * n_iter), $t_0$ определяется на основе эвристики, предложенной Леоном Ботту, так что ожидаемые начальные обновления сопоставимы с ожидаемым размером весов (это предполагает, что норма обучающих выборок составляет приблизительно 1). Точное определение можно найти _init_t в BaseSGD.

Для регрессии график скорости обучения по умолчанию — обратное масштабирование ( learning_rate='invscaling'), заданное как
$$\eta^{(t)} = \frac{eta_0}{t^{power_t}}$$

где $eta_0$ а также $power_t$- гиперпараметры, выбираемые пользователем с помощью eta0 и power_t, соответственно.

Для постоянной скорости обучения используйте learning_rate='constant' и используйте, eta0 чтобы указать скорость обучения.

Для адаптивного уменьшения скорости обучения используйте learning_rate='adaptive' и используйте eta0, чтобы указать начальную скорость обучения. Когда критерий остановки достигнут, скорость обучения делится на 5, и алгоритм не останавливается. Алгоритм останавливается, когда скорость обучения опускается ниже 1e-6.

Параметры модели могут быть доступны через coef_ и intercept_ атрибуты: coef_ держат весыwи intercept_ держит $b$.

При использовании усредненного SGD (с average параметром) coef_ устанавливается средний вес по всем обновлениям:coef_ $= \frac{1}{T} \sum_{t=0}^{T-1} w^{(t)}$, где $T$ это общее количество обновлений, найденных в t_ атрибуте.

1.5.8. Детали реализации

Реализация SGD находится под влиянием Stochastic Gradient из 7 . Подобно SvmSGD, вектор весов представлен как произведение скаляра и вектора, что позволяет эффективно обновлять вес в случае регуляризации L2. В случае разреженного ввода перехват обновляется с меньшей скоростью обучения (умноженной на 0,01), чтобы учесть тот факт, что он обновляется чаще. Примеры обучения выбираются последовательно, и скорость обучения снижается после каждого наблюдаемого примера. Мы приняли график скорости обучения от 8 . Для мультиклассовой классификации используется подход «один против всех». Мы используем алгоритм усеченного градиента, предложенный в 9 для регуляризации L1 (и эластичной сети). Код написан на Cython.