1.7. Гауссовские процессы ¶

Гауссовские процессы (GP) — это общий метод обучения с учителем, разработанный для решения задач регрессии и вероятностной классификации .

Преимущества гауссовских процессов:

Прогноз интерполирует наблюдения (по крайней мере, для обычных ядер).
Прогноз является вероятностным (гауссовским), так что можно вычислить эмпирические доверительные интервалы и на их основе решить, следует ли корректировать (онлайн-подгонка, адаптивная подгонка) прогноз в некоторой интересующей области.
Универсальность: можно указать разные ядра . Предоставляются общие ядра, но также можно указать собственные ядра.

К недостаткам гауссовских процессов можно отнести:

Они не являются разреженными, т. Е. Они используют всю информацию об образцах / характеристиках для выполнения прогноза.
Они теряют эффективность в пространствах больших размеров, а именно, когда количество функций превышает несколько десятков.

1.7.1. Регрессия гауссовского процесса (GPR)

В GaussianProcessRegressor реализует гауссовских процессов (GP) для целей регрессии. Для этого необходимо указать предшествующего врача общей практики. Предполагается, что предыдущее среднее значение является постоянным и нулевым (для normalize_y=False) или средним значением обучающих данных (для normalize_y=True). Ковариация предшествующего уровня определяется передачей объекта ядра . Гиперпараметры ядра оптимизируются во время подгонки GaussianProcessRegressor за счет максимизации логарифмического маржинального правдоподобия (LML) на основе переданного optimizer. Поскольку LML может иметь несколько локальных оптимизаций, оптимизатор можно запускать повторно, указав n_restarts_optimizer. Первый запуск всегда выполняется, начиная с начальных значений гиперпараметров ядра; последующие прогоны проводятся на основе значений гиперпараметров, выбранных случайным образом из диапазона допустимых значений. Если исходные гиперпараметры должны быть фиксированными, None может быть передан как оптимизатор.

Уровень шума в целях можно указать, передав его через параметр alpha, либо глобально как скаляр, либо для каждой точки данных. Обратите внимание, что умеренный уровень шума также может быть полезен для решения числовых проблем во время подгонки, поскольку он эффективно реализуется как регуляризация Тихонова, то есть путем добавления его к диагонали матрицы ядра. Альтернативой явному указанию уровня шума является включение в ядро компонента WhiteKernel, который может оценивать глобальный уровень шума по данным (см. Пример ниже).

Реализация основана на алгоритме 2.1 [RW2006] . В дополнение к API стандартных оценщиков scikit-learn, GaussianProcessRegressor:

позволяет прогнозировать без предварительной подгонки (на основе предшествующего GP)
предоставляет дополнительный метод sample_y(X), который оценивает образцы, взятые из георадара (априорные или апостериорные) при заданных входных данных.
предоставляет метод log_marginal_likelihood(theta), который можно использовать извне для других способов выбора гиперпараметров, например, через цепь Маркова Монте-Карло.

1.7.2. Примеры георадара

1.7.2.1. Георадар с оценкой уровня шума

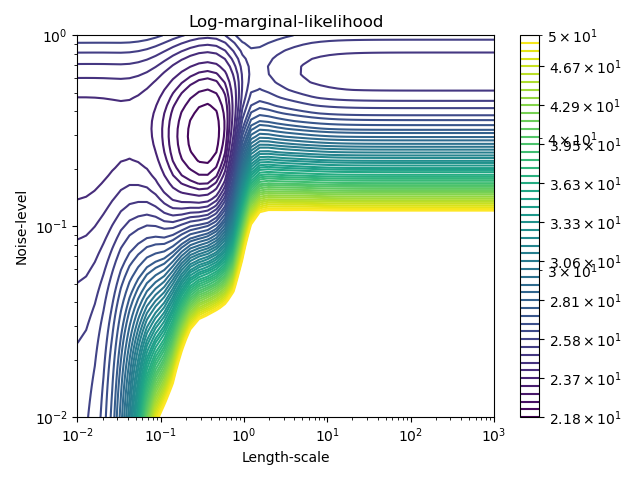
Этот пример показывает, что георадар с суммирующим ядром, включающим WhiteKernel, может оценить уровень шума данных. Иллюстрация ландшафта логарифмического предельного правдоподобия (LML) показывает, что существуют два локальных максимума LML.

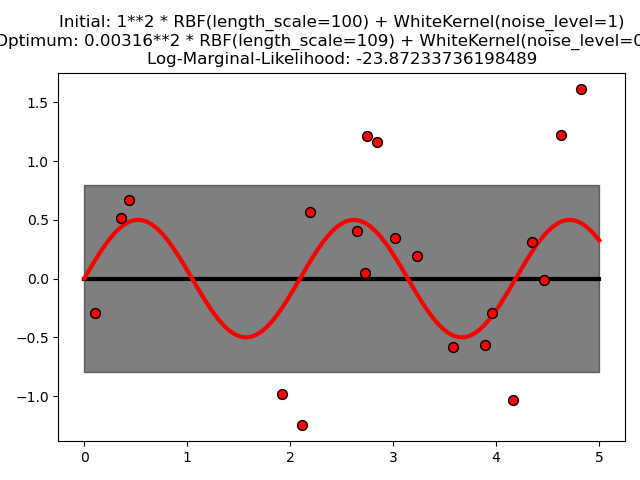
Первый соответствует модели с высоким уровнем шума и большим масштабом длины, которая объясняет все вариации данных шумом.

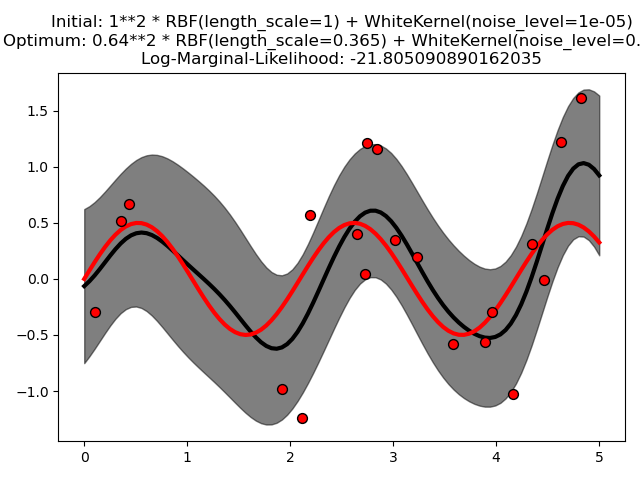
Второй вариант имеет меньший уровень шума и более короткую шкалу длины, что объясняет большую часть вариации функциональной зависимостью без шума. Вторая модель имеет более высокую вероятность; однако, в зависимости от начального значения гиперпараметров, оптимизация на основе градиента также может сходиться к решению с высоким уровнем шума. Таким образом, важно повторить оптимизацию несколько раз для разных инициализаций.

1.7.2.2. Сравнение GPR и ядра Ридж регрессии

И регрессия гребня ядра (KRR), и GPR изучают целевую функцию, используя внутренне «трюк с ядром». KRR изучает линейную функцию в пространстве, индуцированную соответствующим ядром, которая соответствует нелинейной функции в исходном пространстве. Линейная функция в пространстве ядра выбирается на основе среднеквадратичной потери ошибки с регуляризацией гребня. GPR использует ядро для определения ковариации предварительного распределения по целевым функциям и использует наблюдаемые обучающие данные для определения функции правдоподобия. На основе теоремы Байеса определяется (гауссово) апостериорное распределение по целевым функциям, среднее значение которого используется для прогнозирования.

Основное различие состоит в том, что GPR может выбирать гиперпараметры ядра на основе градиентного подъема на функции предельного правдоподобия, в то время как KRR должен выполнять поиск по сетке с перекрестно проверенной функцией потерь (среднеквадратичная потеря ошибки). Еще одно отличие состоит в том, что GPR изучает генеративную вероятностную модель целевой функции и, таким образом, может предоставлять значимые доверительные интервалы и апостериорные выборки вместе с прогнозами, в то время как KRR предоставляет только прогнозы.

На следующем рисунке показаны оба метода на искусственном наборе данных, который состоит из синусоидальной целевой функции и сильного шума. На рисунке сравнивается изученная модель KRR и GPR на основе ядра ExpSineSquared, которое подходит для обучения периодических функций. Гиперпараметры ядра управляют гладкостью (length_scale) и периодичностью ядра (периодичностью). Более того, уровень шума данных явно определяется GPR с помощью дополнительного компонента WhiteKernel в ядре и параметра регуляризации альфа KRR.

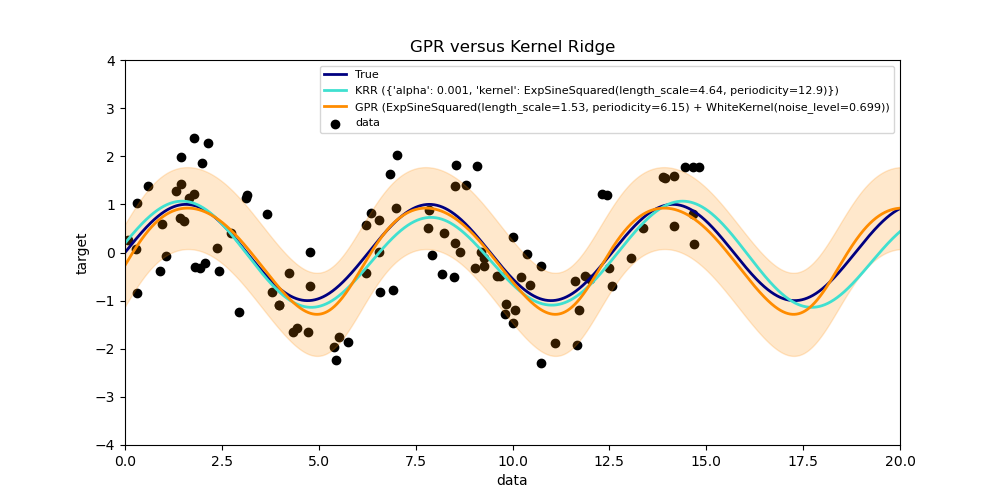
Рисунок показывает, что оба метода изучают разумные модели целевой функции. GPR правильно определяет периодичность функции, чтобы примерно $2∗\pi$ (6.28), а KRR выбирает удвоенную периодичность $4∗\pi$. Кроме того, GPR обеспечивает разумные пределы достоверности прогноза, которые недоступны для KRR. Основное различие между этими двумя методами — время, необходимое для подбора и прогнозирования: хотя подгонка KRR в принципе выполняется быстро, поиск по сетке для оптимизации гиперпараметров экспоненциально масштабируется с увеличением числа гиперпараметров («проклятие размерности»). Оптимизация параметров на основе градиента в GPR не страдает от этого экспоненциального масштабирования и, таким образом, значительно быстрее в этом примере с трехмерным пространством гиперпараметров. Время для прогнозирования аналогично; однако создание дисперсии прогнозируемого распределения GPR занимает значительно больше времени, чем просто прогнозирование среднего значения.

1.7.2.3. Георадар по данным CO2 на Мауна-Лоа

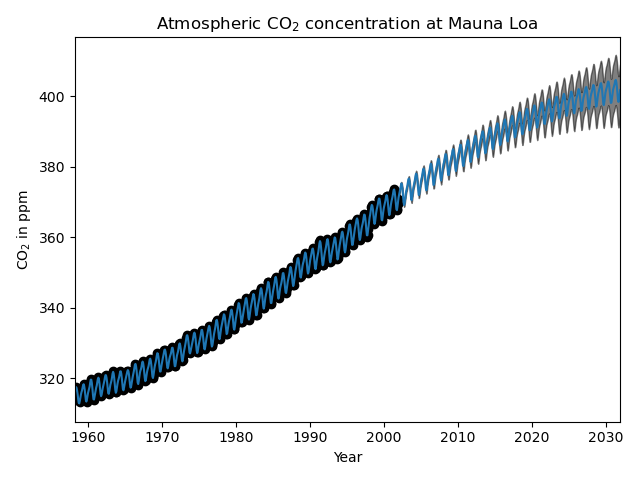
Этот пример основан на Разделе 5.4.3 [RW2006] . Он иллюстрирует пример комплексной разработки ядра и оптимизации гиперпараметров с использованием градиентного подъема на логарифмическом предельном правдоподобии. Данные состоят из среднемесячных концентраций CO2 в атмосфере (в частях на миллион по объему (ppmv)), собранных в обсерватории Мауна-Лоа на Гавайях в период с 1958 по 1997 год. Цель состоит в моделировании концентрации CO2 как функции времени t .

Ядро состоит из нескольких терминов, которые отвечают за объяснение различных свойств сигнала:

долгосрочный плавный восходящий тренд следует объяснить ядром RBF. Ядро RBF с большим масштабом длины заставляет этот компонент быть гладким; не является обязательным, что тенденция растет, что оставляет этот выбор за GP. Конкретный масштаб длины и амплитуда являются свободными гиперпараметрами.
сезонная составляющая, которую следует объяснить периодическим ядром ExpSineSquared с фиксированной периодичностью в 1 год. Масштаб длины этой периодической составляющей, контролирующий ее гладкость, является свободным параметром. Чтобы позволить распаду от точной периодичности, берется продукт с ядром RBF. Масштаб длины этого компонента RBF контролирует время затухания и является дополнительным свободным параметром.
более мелкие, среднесрочные неоднородности должны быть объяснены компонентом ядра RationalQuadratic, масштаб длины и параметр альфа которого, которые определяют размытость масштабов длины, должны быть определены. Согласно [RW2006] , эти нарушения могут быть лучше объяснены RationalQuadratic, чем компонентом ядра RBF, вероятно, потому, что он может приспособиться к нескольким масштабам длины.
термин «шум», состоящий из вклада ядра RBF, который должен объяснять коррелированные компоненты шума, такие как местные погодные явления, и вклад WhiteKernel для белого шума. Относительные амплитуды и масштаб длины RBF являются дополнительными свободными параметрами.

Максимизация логарифма маржинального правдоподобия после вычитания целевого среднего дает следующее ядро с LML -83,214:

34.4**2 * RBF(length_scale=41.8)
+ 3.27**2 * RBF(length_scale=180) * ExpSineSquared(length_scale=1.44,
                                                   periodicity=1)
+ 0.446**2 * RationalQuadratic(alpha=17.7, length_scale=0.957)
+ 0.197**2 * RBF(length_scale=0.138) + WhiteKernel(noise_level=0.0336)

Таким образом, большая часть целевого сигнала (34,4 ppm) объясняется долгосрочным восходящим трендом (длительность 41,8 года). Периодическая составляющая имеет амплитуду 3,27 частей на миллион, время распада 180 лет и масштаб длины 1,44. Длительное время спада указывает на то, что у нас есть локально очень близкая к периодической сезонная составляющая. Коррелированный шум имеет амплитуду 0,197 ppm с масштабом длины 0,138 лет и вклад белого шума 0,197 ppm. Таким образом, общий уровень шума очень мал, что указывает на то, что данные могут быть очень хорошо объяснены моделью. Рисунок также показывает, что модель делает очень уверенные прогнозы примерно до 2015 года.

1.7.3. Классификация гауссовских процессов (GPC)

В GaussianProcessClassifier реализует гауссовские процессы (GP) для целей классификации, более конкретно для вероятностной классификации, где тест предсказания принимают форму класса вероятностей. GaussianProcessClassifier помещает GP перед скрытой функцией $f$, который затем сжимается с помощью функции связи для получения вероятностной классификации. Скрытая функция $f$ это так называемая мешающая функция, значения которой не наблюдаются и не имеют значения сами по себе. Его цель состоит в том, чтобы позволить удобную формулировку модели, и $f$ удаляется (интегрируется) во время прогнозирования. GaussianProcessClassifier реализует функцию логистической связи, для которой интеграл не может быть вычислен аналитически, но легко аппроксимируется в двоичном случае.

В отличие от настройки регрессии, задняя часть скрытой функции $f$ не является гауссовым даже для априорного GP, поскольку гауссовское правдоподобие не подходит для меток дискретных классов. Вместо этого используется негауссовское правдоподобие, соответствующее функции логистической связи (логит). GaussianProcessClassifier аппроксимирует негауссовское апостериорное значение с помощью гауссова на основе приближения Лапласа. Более подробную информацию можно найти в главе 3 [RW2006] .

Предполагается, что априорное среднее значение GP равно нулю. Ковариация предшествующего уровня определяется передачей объекта ядра . Гиперпараметры ядра оптимизируются во время подгонки GaussianProcessRegressor за счет максимизации логарифмического маржинального правдоподобия (LML) на основе переданного optimizer. Поскольку LML может иметь несколько локальных оптимизаций, оптимизатор можно запускать повторно, указав n_restarts_optimizer. Первый запуск всегда выполняется, начиная с начальных значений гиперпараметров ядра; последующие прогоны проводятся на основе значений гиперпараметров, выбранных случайным образом из диапазона допустимых значений. Если исходные гиперпараметры должны быть фиксированными, None может быть передан как оптимизатор.

GaussianProcessClassifier поддерживает мультиклассовую классификацию, выполняя обучение и прогнозирование по принципу «один против остальных» или «один против одного». В режиме «один против остальных» для каждого класса устанавливается один бинарный гауссовский классификатор процессов, который обучается отделять этот класс от остальных. В «one_vs_one» для каждой пары классов устанавливается один бинарный гауссовский классификатор процессов, который обучен разделять эти два класса. Предсказания этих двоичных предикторов объединяются в многоклассовые прогнозы. См. Более подробную информацию в разделе о мультиклассовой классификации .

В случае классификации гауссовского процесса «one_vs_one» может быть дешевле в вычислительном отношении, поскольку он должен решать многие проблемы, включающие только подмножество всего обучающего набора, а не меньшее количество проблем во всем наборе данных. Поскольку классификация процессов по Гауссу кубически масштабируется в зависимости от размера набора данных, это может быть значительно быстрее. Однако обратите внимание, что «one_vs_one» не поддерживает прогнозирование оценок вероятности, а только простые прогнозы. Более того, обратите внимание, что GaussianProcessClassifier (пока) не реализовано истинное мультиклассовое приближение Лапласа внутри, но, как обсуждалось выше, оно основано на внутреннем решении нескольких задач двоичной классификации, которые комбинируются с использованием одного против остальных или одного против одного.

1.7.4. Примеры GPC

1.7.4.1. Вероятностные прогнозы с GPC

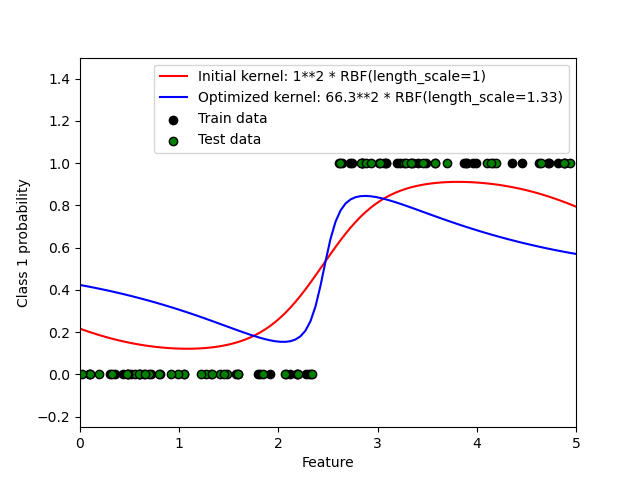
Этот пример иллюстрирует прогнозируемую вероятность GPC для ядра RBF с различными вариантами гиперпараметров. На первом рисунке показана прогнозируемая вероятность GPC с произвольно выбранными гиперпараметрами и с гиперпараметрами, соответствующими максимальному логарифмическому маржинальному правдоподобию (LML).

Хотя гиперпараметры, выбранные путем оптимизации LML, имеют значительно больший LML, они работают немного хуже в соответствии с потерями журнала на тестовых данных. На рисунке показано, что это происходит потому, что они демонстрируют резкое изменение вероятностей классов на границах классов (что хорошо), но имеют прогнозируемые вероятности, близкие к 0,5, вдали от границ классов (что плохо). Этот нежелательный эффект вызван Приближение Лапласа, используемое внутри GPC.

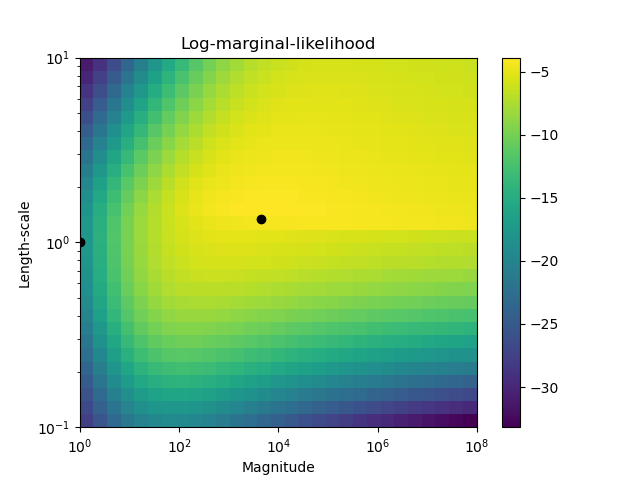
На втором рисунке показана логарифмическая маргинальная вероятность для различных вариантов выбора гиперпараметров ядра, при этом два варианта гиперпараметров, используемых на первом рисунке, выделены черными точками.

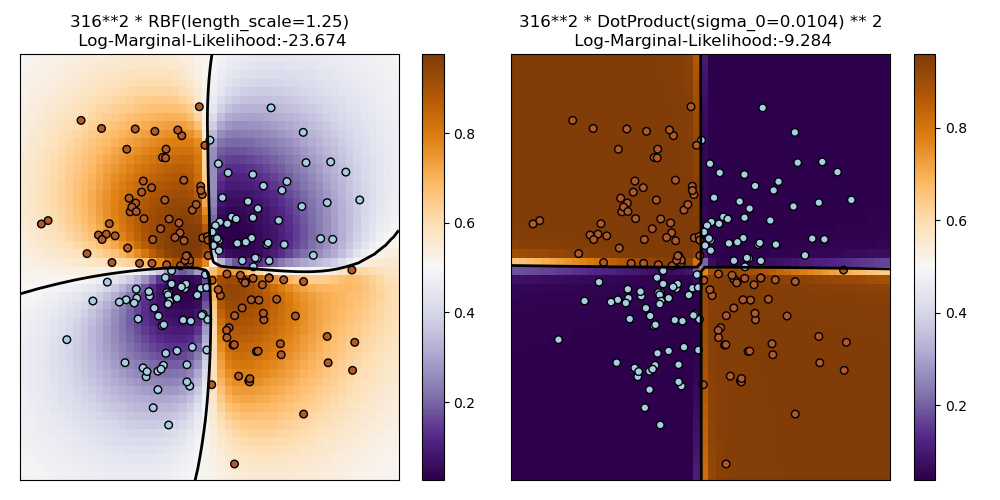
1.7.4.2. Иллюстрация GPC в наборе данных XOR

Этот пример иллюстрирует GPC для данных XOR. Сравниваются стационарное изотропное ядро (RBF) и нестационарное ядро ( DotProduct). На этом конкретном наборе данных DotProduct ядро получает значительно лучшие результаты, потому что границы классов линейны и совпадают с осями координат. На практике, однако, такие стационарные ядра RBF часто дают лучшие результаты.

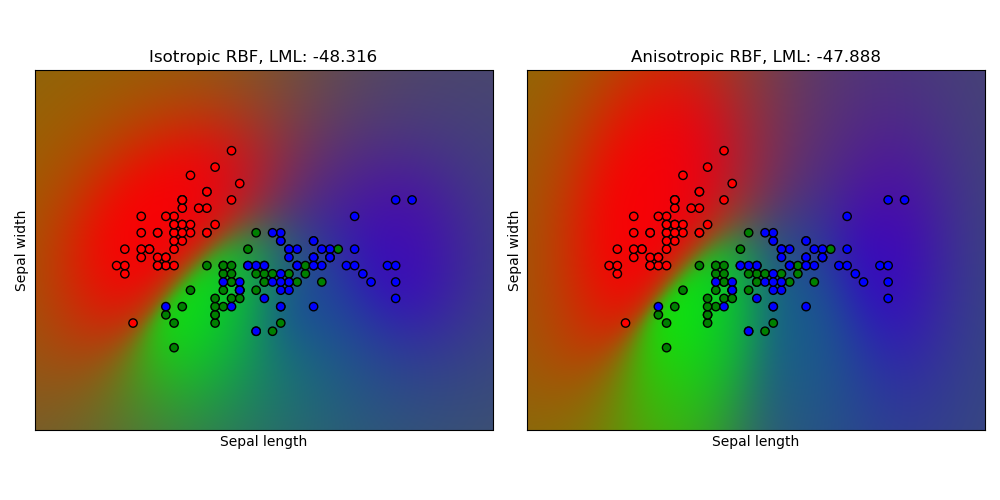
1.7.4.3. Классификация процессов по Гауссу (GPC) на наборе данных радужной оболочки

Этот пример иллюстрирует прогнозируемую вероятность GPC для изотропного и анизотропного ядра RBF в двумерной версии для набора данных iris. Это иллюстрирует применимость GPC к небинарной классификации. Анизотропное ядро RBF получает немного более высокое логарифмическое маргинальное правдоподобие за счет присвоения разных масштабов длины двум размерам признаков.

1.7.5. Ядра для гауссовских процессов

Ядра (также называемые «ковариационными функциями» в контексте GP) являются важнейшим компонентом GP, которые определяют форму предшествующих и апостериорных функций GP. Они кодируют предположения об изучаемой функции, определяя «сходство» двух точек данных в сочетании с предположением, что аналогичные точки данных должны иметь аналогичные целевые значения. Можно выделить две категории ядер: стационарные ядра зависят только от расстояния двух точек данных, а не от их абсолютных значений $k(x_i, x_j)= k(d(x_i, x_j))$ и, таким образом, инвариантны к трансляциям во входном пространстве, в то время как нестационарные ядра зависят также от конкретных значений точек данных. Стационарные ядра могут быть далее подразделены на изотропные и анизотропные ядра, где изотропные ядра также инвариантны к поворотам во входном пространстве. Для получения дополнительных сведений см. Главу 4 [RW2006] . Чтобы узнать, как лучше всего комбинировать разные ядра, обратитесь к [Duv2014] .

1.7.5.1. API ядра гауссовского процесса

Основное использование a Kernel— вычисление ковариации GP между точками данных. Для этого __call__ можно вызвать метод ядра. Этот метод можно использовать либо для вычисления «автоковариации» всех пар точек данных в 2-м массиве X, либо «кросс-ковариации» всех комбинаций точек данных 2-го массива X с точками данных в 2-м массиве Y. Для всех ядер k (кроме WhiteKernel) справедливо следующее тождество: k(X) == K(X, Y=X)

Если используется только диагональ diag() автоковариации, может быть вызван метод ядра, который более эффективен с точки зрения вычислений, чем эквивалентный вызов __call__: np.diag(k(X, X)) == k.diag(X)

Ядра параметризованы вектором $\theta$ гиперпараметров. Эти гиперпараметры могут, например, управлять масштабами длины или периодичностью ядра (см. Ниже). Все ядра поддерживают вычисление аналитических градиентов автоковариантности ядра по отношению к $\log(\theta)$ через настройку eval_gradient=True в __call__ методе. То есть возвращается массив, в котором запись содержит(len(X), len(X), len(theta))[i, j, l] $\frac{\partial k_\theta(x_i, x_j)}{\partial log(\theta_l)}$. Этот градиент используется гауссовским процессом (как регрессором, так и классификатором) при вычислении градиента логарифмического предельного правдоподобия, который, в свою очередь, используется для определения значения $\theta$, который максимизирует предельное логарифмическое правдоподобие за счет градиентного подъема. Для каждого гиперпараметра необходимо указать начальное значение и границы при создании экземпляра ядра. Текущее значение $\theta$ можно получить и установить через свойство theta объекта ядра. Более того, границы гиперпараметров могут быть доступны через свойство bounds ядра. Обратите внимание, что оба свойства (тета и границы) возвращают преобразованные в журнал значения внутренних значений, поскольку они обычно более поддаются оптимизации на основе градиента. Спецификация каждого гиперпараметра хранится в форме экземпляра Hyperparameter в соответствующем ядре. Обратите внимание, что ядро, использующее гиперпараметр с именем «x», должно иметь атрибуты self.x и self.x_bounds.

Абстрактный базовый класс для всех ядер — Kernel. Ядро реализует подобный интерфейс , как Estimator, обеспечивая методы get_params(), set_params()и clone(). Это позволяет также устанавливать значения ядра с помощью мета-оценок, таких как Pipeline или GridSearch. Обратите внимание, что из-за вложенной структуры ядер (путем применения операторов ядра, см. Ниже) имена параметров ядра могут стать относительно сложными. Как правило, для бинарного оператора ядра параметры левого операнда имеют префикс, k1__ а параметры правого операнда — k2__. Дополнительный удобный метод clone_with_theta(theta), который возвращает клонированную версию ядра, но с гиперпараметрами, установленными на theta. Наглядный пример:

>>> from sklearn.gaussian_process.kernels import ConstantKernel, RBF
>>> kernel = ConstantKernel(constant_value=1.0, constant_value_bounds=(0.0, 10.0)) * RBF(length_scale=0.5, length_scale_bounds=(0.0, 10.0)) + RBF(length_scale=2.0, length_scale_bounds=(0.0, 10.0))
>>> for hyperparameter in kernel.hyperparameters: print(hyperparameter)
Hyperparameter(name='k1__k1__constant_value', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k1__k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
>>> params = kernel.get_params()
>>> for key in sorted(params): print("%s : %s" % (key, params[key]))
k1 : 1**2 * RBF(length_scale=0.5)
k1__k1 : 1**2
k1__k1__constant_value : 1.0
k1__k1__constant_value_bounds : (0.0, 10.0)
k1__k2 : RBF(length_scale=0.5)
k1__k2__length_scale : 0.5
k1__k2__length_scale_bounds : (0.0, 10.0)
k2 : RBF(length_scale=2)
k2__length_scale : 2.0
k2__length_scale_bounds : (0.0, 10.0)
>>> print(kernel.theta)  # Note: log-transformed
[ 0.         -0.69314718  0.69314718]
>>> print(kernel.bounds)  # Note: log-transformed
[[      -inf 2.30258509]
 [      -inf 2.30258509]
 [      -inf 2.30258509]]

Все ядра гауссовских процессов совместимы sklearn.metrics.pairwise и наоборот: экземпляры подклассов Kernel могут передаваться как metricв pairwise_kernels из sklearn.metrics.pairwise. Более того, попарные функции ядра могут использоваться как ядра GP с помощью класса-оболочки PairwiseKernel. Единственное предостережение заключается в том, что градиент гиперпараметров не аналитический, а числовой, и все эти ядра поддерживают только изотропные расстояния. Параметр gammaсчитается гиперпараметром и может быть оптимизирован. Остальные параметры ядра устанавливаются непосредственно при инициализации и остаются неизменными.

1.7.5.2. Базовые ядра

Ядро ConstantKernel может быть использовано как часть Product ядра, где он масштабирует величину других фактора (ядра) или как часть Sum ядра, где она изменяет среднее значение гауссовского процесса. Это зависит от параметра $constant_value$. Это определяется как:
$$k(x_i, x_j) = constant_value \;\forall\; x_1, x_2$$

Основной вариант использования WhiteKernel ядра — это часть ядра суммы, где оно объясняет шумовую составляющую сигнала. Настройка его параметра $noise_level$ соответствует оценке уровня шума. Это определяется как:
$$k(x_i, x_j) = noise_level \text{ if } x_i == x_j \text{ else } 0$$

1.7.5.3. Операторы ядра

Операторы ядра берут одно или два базовых ядра и объединяют их в новое ядро. Ядро Sum имеет два ядра $k_1$ а также $k_2$ и объединяет их через $k_{sum}(X,Y)=k_{1}(X,Y)+k_{2}(X,Y)$. Ядро Product имеет два ядра $k_1$ а также $k_2$ и объединяет их через $k_{product}(X,Y)=k_{1}(X,Y)∗k_{2}(X,Y)$. Ядро Exponentiation занимает одну базового ядро и скалярный параметрp и объединяет их через $k_{exp}(X,Y)=k(X,Y)^p$. Обратите внимание , что методы магии __add__, __mul___и __pow__ замещаются в ядре объектов, таким образом, можно использовать , например RBF() + RBF(), в качестве ярлыка для Sum(RBF(), RBF())

1.7.5.4. Ядро радиально-базисной функции (РБФ)

Ядро RBF является стационарным ядром. Он также известен как «квадрат экспоненциального» ядра. Параметризуется параметром масштаба длины $l>0$, который может быть либо скаляром (изотропный вариант ядра), либо вектором с тем же числом измерений, что и входные данные. x(анизотропный вариант ядра). Ядро выдается:
$$k(x_i, x_j) = \text{exp}\left(- \frac{d(x_i, x_j)^2}{2l^2} \right)$$

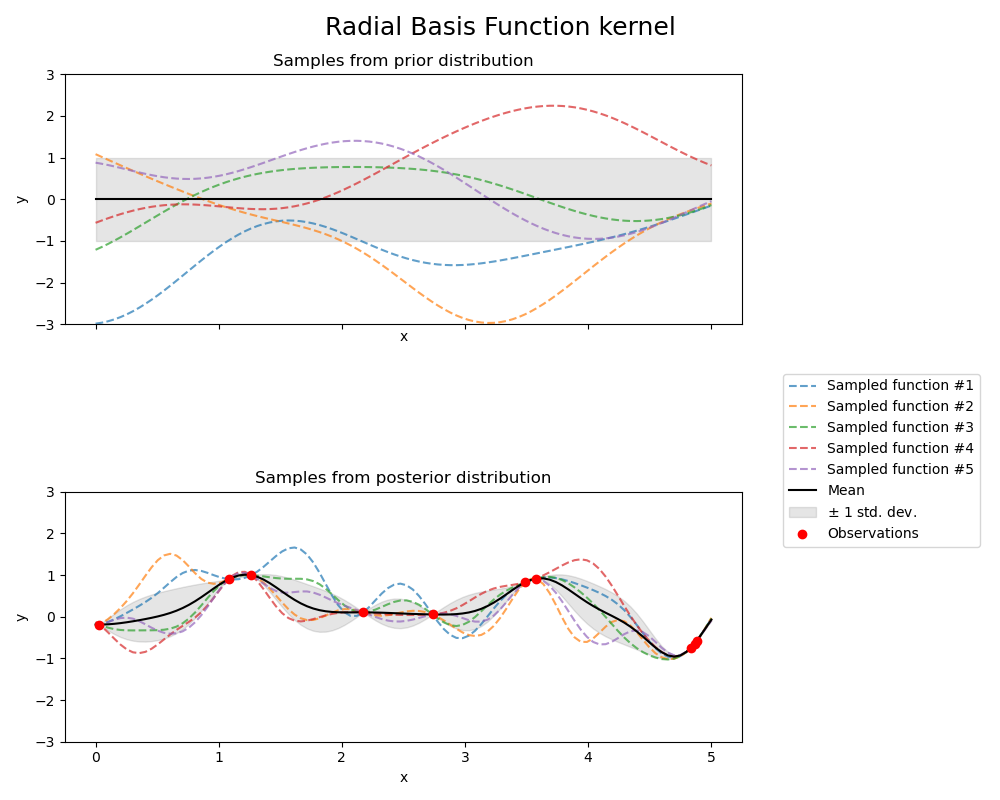
где $d(\cdot, \cdot)$- евклидово расстояние. Это ядро бесконечно дифференцируемо, что означает, что GP с этим ядром в качестве ковариационной функции имеют среднеквадратичные производные всех порядков и, таким образом, очень гладкие. На следующем рисунке показаны предшествующие и последующие точки GP, являющиеся результатом ядра RBF:

1.7.5.5. Ядро Матерна

Ядро Matern является стационарным ядром и обобщение RBF ядра. Имеет дополнительный параметрνкоторый контролирует гладкость результирующей функции. Параметризуется параметром масштаба длины $l>0$, который может быть либо скаляром (изотропный вариант ядра), либо вектором с тем же числом измерений, что и входные данные $x$ (анизотропный вариант ядра). Ядро выдается:
$$k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)^\nu K_\nu\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg),$$

где $d(\cdot,\cdot)$ — евклидово расстояние, $K_\nu(\cdot)$ является модифицированной функцией Бесселя и $\Gamma(\cdot)$ это гамма-функция. В виде $\nu\rightarrow\infty$, ядро Матерна сходится к ядру RBF. Когда $\nu = 1/2$, ядро Матерна становится идентичным абсолютному экспоненциальному ядру, т. е.
$$k(x_i, x_j) = \exp \Bigg(- \frac{1}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{1}{2}$$

В частности, $\nu = 3/2$:
$$k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{3}}{l} d(x_i , x_j )\Bigg) \exp \Bigg(-\frac{\sqrt{3}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{3}{2}$$

а также $\nu = 5/2$:
$$k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{5}}{l} d(x_i , x_j ) +\frac{5}{3l} d(x_i , x_j )^2 \Bigg) \exp \Bigg(-\frac{\sqrt{5}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{5}{2}$$

являются популярным выбором для обучения функциям, которые не являются бесконечно дифференцируемыми (как предполагает ядро RBF), но хотя бы один раз ($\nu = 3/2$) или дважды дифференцируемые ($\nu = 5/2$).

Гибкость управления плавностью заученной функции с помощью $\nu$ позволяет адаптироваться к свойствам истинного базового функционального отношения. Априорный и апостериорный GP, полученный из ядра Матерна, показаны на следующем рисунке:

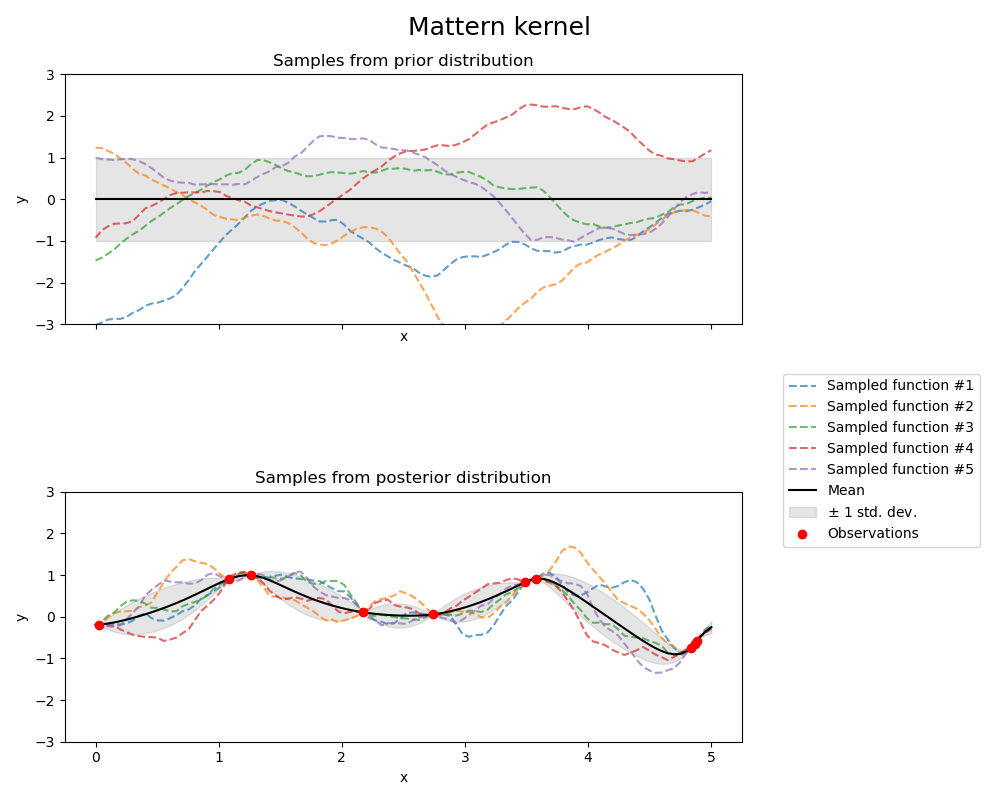
См. [RW2006] , pp84 для получения дополнительной информации о различных вариантах ядра Matérn.

1.7.5.6. Рациональное квадратичное ядро

Ядро RationalQuadratic можно рассматривать как масштаб смесь (бесконечную сумму) RBF ядер с различной характерной длиной чешуей. Параметризуется параметром масштаба длины $l>0$ и параметр масштабной смеси $\alpha>0$ Только изотропный вариант, когда $l$ — скаляр поддерживается в данный момент. Ядро выдается:
$$k(x_i, x_j) = \left(1 + \frac{d(x_i, x_j)^2}{2\alpha l^2}\right)^{-\alpha}$$

На RationalQuadratic следующем рисунке показаны предшествующие и последующие точки GP, полученные в результате ядра:

1.7.5.7. Ядро Exp-Sine-Squared

Ядро ExpSineSquared позволяет моделировать периодические функции. Параметризуется параметром масштаба длины $l>0$ и параметр периодичности $p>0$. Только изотропный вариант, когда $l$ — скаляр поддерживается в данный момент. Ядро выдается:
$$k(x_i, x_j) = \text{exp}\left(- \frac{ 2\sin^2(\pi d(x_i, x_j) / p) }{ l^ 2} \right)$$

Предыдущий и последующий GP, полученный в результате ядра ExpSineSquared, показаны на следующем рисунке:

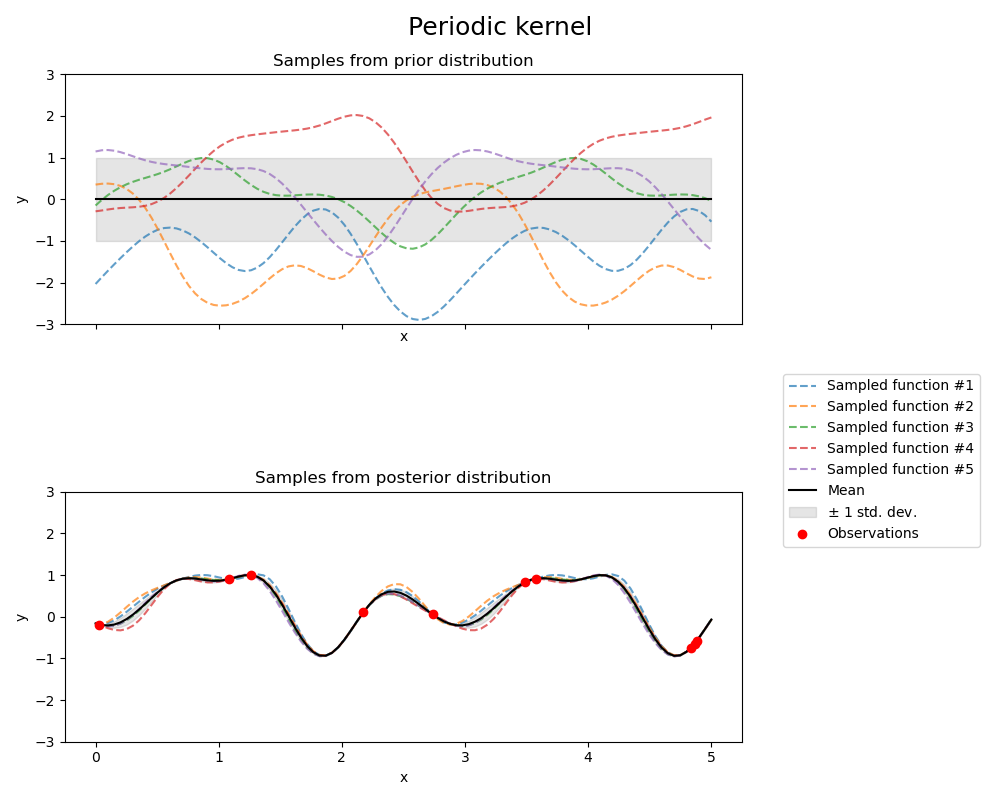
1.7.5.8. Ядро скалярного произведения

Ядро DotProduct не является стационарным и может быть получено из линейной регрессии, полагая $N(0, 1)$ априорные значения коэффициентов при $x_d (d = 1, . . . , D)$ и приор $N(0, \sigma_0^2)$ по предвзятости. Ядро DotProduct инвариантно к вращению координат вокруг начала координат, но не переводы. Параметризуется параметром $\sigma_0^2$. Для $\sigma_0^2 = 0$, ядро называется однородным линейным ядром, иначе оно неоднородно. Ядро дается формулой
$$k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j$$

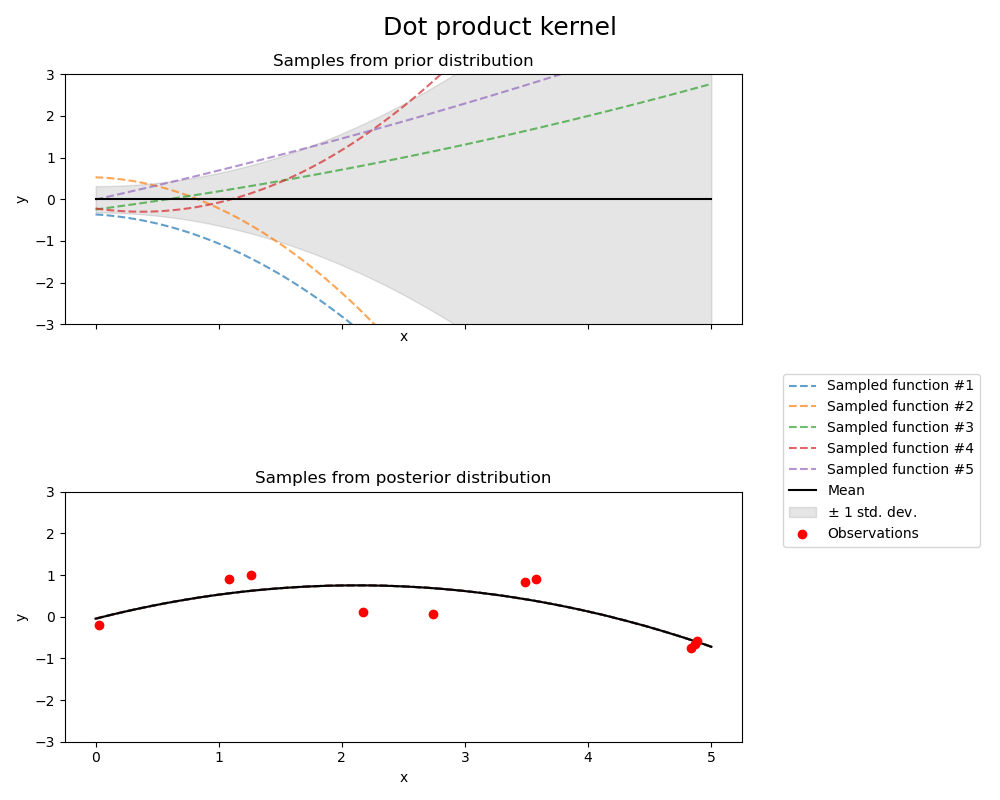
Ядро DotProduct обычно сочетается с потенцированием. Пример с показателем степени 2 показан на следующем рисунке:

1.7.5.9. Ссылки

RW2006 Карл Эдуард Расмуссен и Кристофер К.И. Уильямс, «Гауссовские процессы для машинного обучения», MIT Press, 2006 г. Ссылка на официальную полную версию книги в формате PDF здесь .

Duv2014 Дэвид Дювено, «Поваренная книга ядра: советы по ковариационным функциям», 2014 г., ссылка .