2.2. Обучение многообразию ¶
Ищите самое необходимое
Самые простые предметы первой необходимости
Забудь о своих заботах и ссорах
Я имею в виду самое необходимое
Рецепты древней матери-природы
Это приносит самое необходимое для жизни
— Песня Балу [Книга джунглей]
2.2.1. Введение
Наборы данных большой размерности может быть очень трудно визуализировать. В то время как данные в двух или трех измерениях могут быть построены для отображения внутренней структуры данных, эквивалентные многомерные графики гораздо менее интуитивно понятны. Чтобы облегчить визуализацию структуры набора данных, необходимо каким-то образом уменьшить размер.
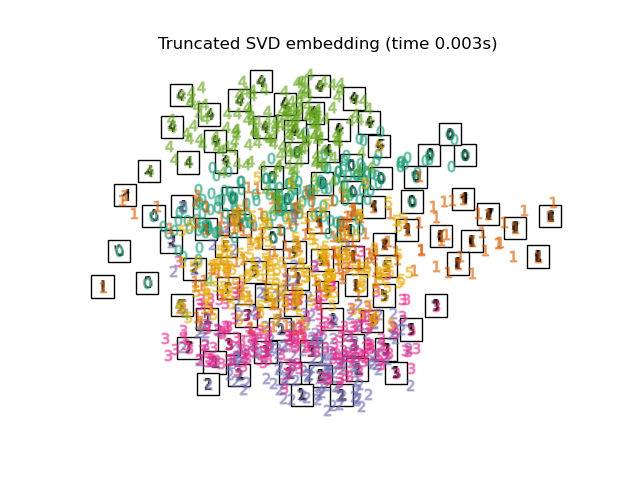
Самый простой способ добиться этого уменьшения размерности — сделать случайную проекцию данных. Хотя это позволяет в некоторой степени визуализировать структуру данных, случайность выбора оставляет желать лучшего. При случайной проекции наиболее интересная структура данных, вероятно, будет потеряна.

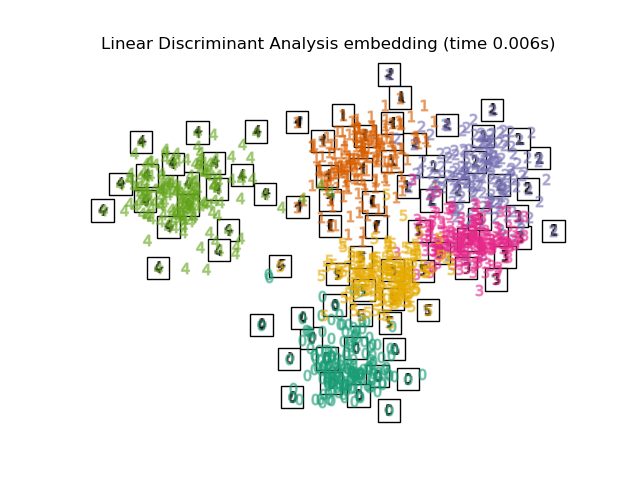
Для решения этой проблемы был разработан ряд контролируемых и неконтролируемых структур снижения линейной размерности, таких как анализ главных компонентов (PCA), независимый компонентный анализ, линейный дискриминантный анализ и другие. Эти алгоритмы определяют конкретные рубрики для выбора «интересной» линейной проекции данных. Эти методы могут быть мощными, но часто упускают важную нелинейную структуру данных.
Manifold Learning можно рассматривать как попытку обобщить линейные структуры, такие как PCA, чтобы они были чувствительны к нелинейной структуре данных. Хотя существуют контролируемые варианты, типичная проблема обучения многообразию не учитывается: она изучает многомерную структуру данных из самих данных без использования заранее определенных классификаций.
Примеры
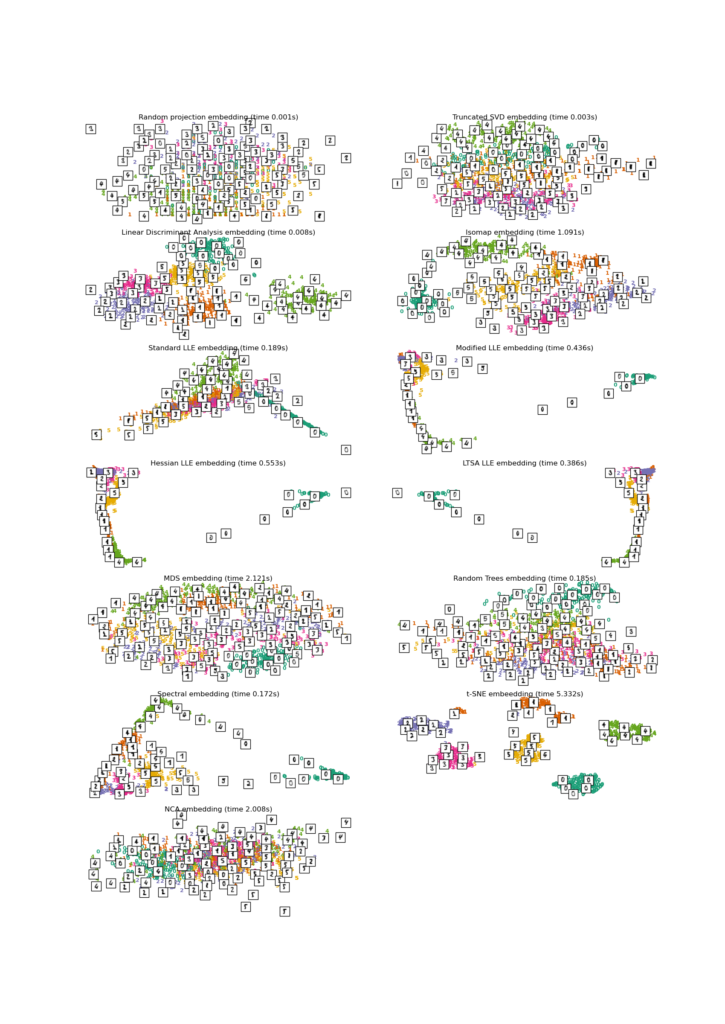
- См. Раздел Обучение многообразию рукописных цифр: локально линейное встраивание, Isomap… для примера уменьшения размерности рукописных цифр.
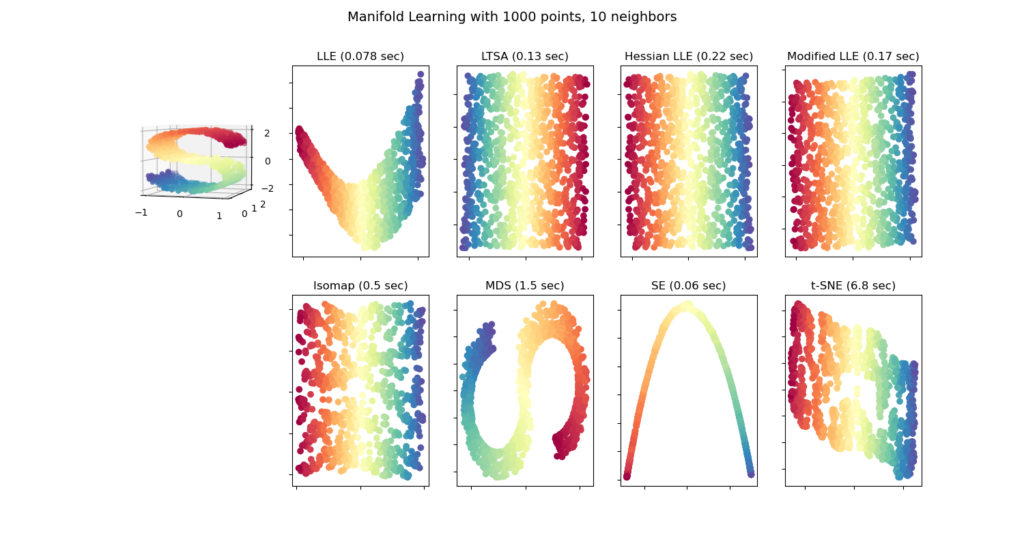
- См. « Сравнение методов обучения многообразию» для примера уменьшения размерности набора данных «S-образная кривая».
Разнообразные реализации обучения, доступные в scikit-learn, приведены ниже.
2.2.2. Isomap
Одним из самых ранних подходов к обучению многообразию является алгоритм Isomap, сокращение от Isometric Mapping. Isomap можно рассматривать как расширение многомерного масштабирования (MDS) или Kernel PCA. Isomap ищет вложение меньшей размерности, которое поддерживает геодезические расстояния между всеми точками. Изокарта может быть выполнена с объектом Isomap.
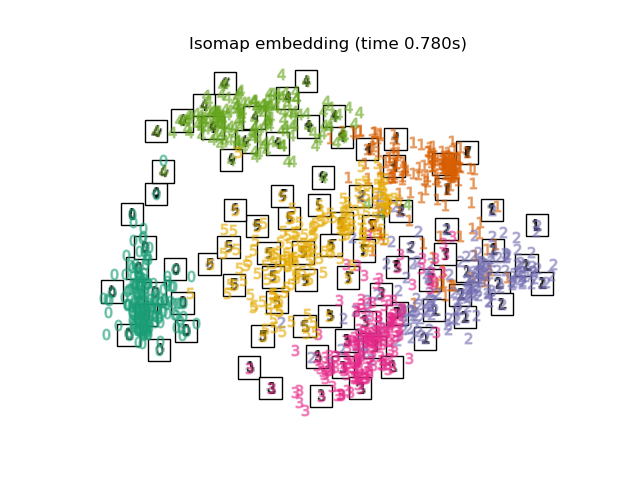
2.2.2.1. Сложность
Алгоритм Isomap состоит из трех этапов:
- Поиск ближайшего соседа. Isomap использует
BallTreeдля эффективного поиска соседей. Стоимость ориентировочно $O[D \log(k) N \log(N)]$, для $k$ ближайшие соседи $N$ указывает в $D$ Габаритные размеры. - Поиск по графу кратчайшего пути. Наиболее эффективными известными алгоритмами для этого являются алгоритм Дейкстры , который приблизительно равен $O[N^2(k + \log(N))]$, или алгоритм Флойда-Уоршалла , который $O[N^3]$. Алгоритм может быть выбран пользователем с
path_methodключевым словомIsomap. Если не указано иное, код пытается выбрать лучший алгоритм для входных данных. - Частичное разложение на собственные значения. Вложение кодируется в собственных векторах, соответствующихd наибольшие собственные значения $N \times N$ ядро isomap. Стоимость плотного решателя составляет примерно $O[d N^2]$. Эту стоимость часто можно уменьшить с помощью
ARPACKрешателя. Собственный преобразователь может быть указан пользователем сeigen_solverключевым словомIsomap. Если не указано иное, код пытается выбрать лучший алгоритм для входных данных.
Общая сложность Isomap составляет $O[D \log(k) N \log(N)] + O[N^2(k + \log(N))] + O[d N^2]$.
- $N$ : количество точек данных обучения
- $D$ : входной размер
- $k$ : количество ближайших соседей
- $d$ : выходной размер
Рекомендации
- «Глобальная геометрическая структура для нелинейного уменьшения размерности» Тененбаум, Дж. Б.; De Silva, V .; И Лэнгфорд, JC Science 290 (5500)
2.2.3. Локально линейное вложение
Локально линейное вложение (LLE) ищет проекцию данных меньшей размерности, которая сохраняет расстояния в пределах локальных окрестностей. Его можно рассматривать как серию локальных анализов главных компонентов, которые сравниваются в глобальном масштабе, чтобы найти лучшее нелинейное вложение.
Локально линейное вложение может быть выполнено с помощью функции locally_linear_embedding или ее объектно-ориентированного аналога LocallyLinearEmbedding.
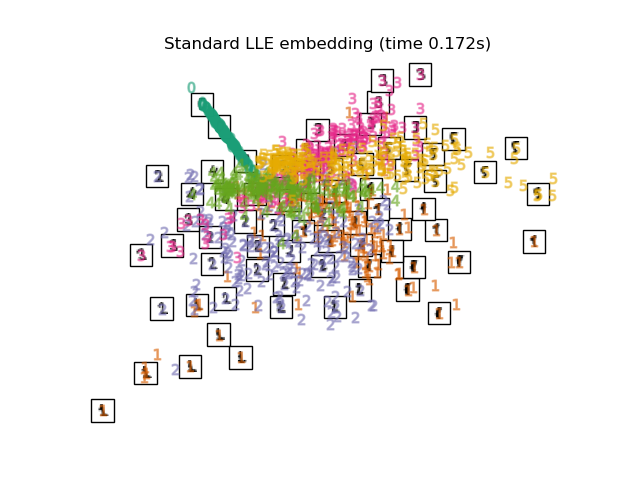
2.2.3.1. Сложность
Стандартный алгоритм LLE состоит из трех этапов:
- Поиск ближайших соседей . См. Обсуждение под Isomap выше.
- Построение весовой матрицы .$O[D N k^3]$. Построение весовой матрицы LLE включает решение $k \times k$ линейное уравнение для каждого из $N$ местные районы
- Частичное разложение на собственные значения . См. Обсуждение под Isomap выше.
Общая сложность стандартного LLE составляет $O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]$.
- $N$ : количество точек данных обучения
- $D$ : входной размер
- $k$ : количество ближайших соседей
- $d$ : выходной размер
Рекомендации
- «Нелинейное уменьшение размерности за счет локально линейного вложения» Роуейс, С. и Саул, Л. Science 290: 2323 (2000)
2.2.4. Модифицированное локально линейное вложение
Одна хорошо известная проблема с LLE — проблема регуляризации. Когда количество соседей больше, чем количество входных измерений, матрица, определяющая каждую локальную окрестность, не имеет ранга. Чтобы решить эту проблему, стандартный LLE применяет произвольный параметр регуляризации.r, который выбирается относительно следа локальной весовой матрицы. Хотя формально можно показать, что как $r \to 0$, решение сходится к желаемому вложению, нет гарантии, что будет найдено оптимальное решение для $r>0$. Эта проблема проявляется во вложениях, которые искажают основную геометрию многообразия.
Одним из способов решения проблемы регуляризации является использование нескольких весовых векторов в каждой окрестности. В этом суть модифицированного локально линейного вложения (MLLE). MLLE может выполняться с помощью функции locally_linear_embedding или ее объектно-ориентированного аналога LocallyLinearEmbedding с ключевым словом method = ‘modified’. Это требует n_neighbors > n_components.
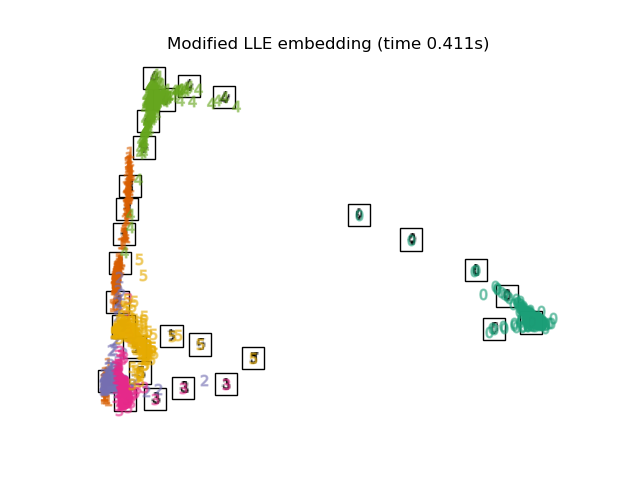
2.2.4.1. Сложность
Алгоритм MLLE состоит из трех этапов:
- Поиск ближайших соседей . То же, что и стандартный LLE
- Построение весовой матрицы . Примерно $O[D N k^3] + O[N (k-D) k^2]$. Первый член в точности эквивалентен стандартному LLE. Второй член связан с построением весовой матрицы из нескольких весов. На практике дополнительные затраты на построение весовой матрицы MLLE относительно невелики по сравнению со стоимостью этапов 1 и 3.
- Частичное разложение на собственные значения . То же, что и стандартный LLE
Общая сложность MLLE составляет $O[D \log(k) N \log(N)] + O[D N k^3] + O[N (k-D) k^2] + O[d N^2]$.
- $N$ : количество точек данных обучения
- $D$ : входной размер
- $k$ : количество ближайших соседей
- $d$ : выходной размер
Рекомендации
2.2.5. Гессенское собственное отображение
Собственное отображение Гессе (также известное как LLE: HLLE на основе Гессе) — еще один метод решения проблемы регуляризации LLE. Он вращается вокруг квадратичной формы на основе гессиана в каждой окрестности, которая используется для восстановления локально линейной структуры. Хотя в других реализациях отмечается его плохое масштабирование с размером данных, sklearn реализованы некоторые алгоритмические улучшения, которые делают его стоимость сопоставимой со стоимостью других вариантов LLE для небольшого размера вывода. HLLE может выполняться с помощью функции locally_linear_embedding или ее объектно-ориентированного аналога LocallyLinearEmbedding с ключевым словом method = ‘hessian’. Это требует n_neighbors > n_components * (n_components + 3) / 2.
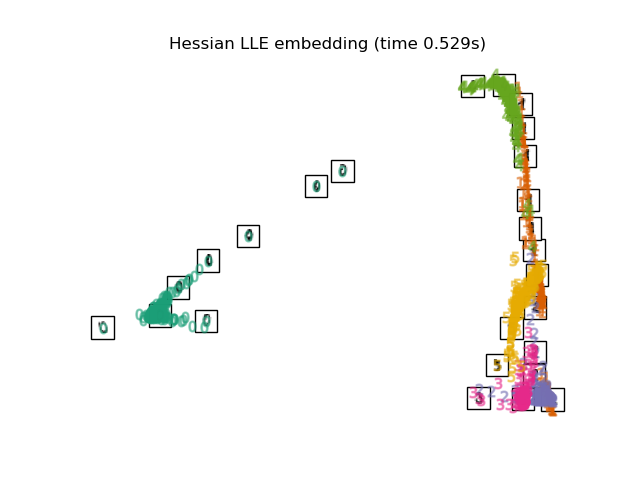
2.2.5.1. Сложность
Алгоритм HLLE состоит из трех этапов:
- Поиск ближайших соседей . То же, что и стандартный LLE
- Построение весовой матрицы . Примерно $O[D N k^3] + O[N d^6]$. Первый член отражает стоимость, аналогичную стоимости стандартного LLE. Второй член получается из QR-разложения локальной оценки гессиана.
- Частичное разложение на собственные значения . То же, что и стандартный LLE
Общая сложность стандартного HLLE составляет $O[D \log(k) N \log(N)] + O[D N k^3] + O[N d^6] + O[d N^2]$.
- $N$ : количество точек данных обучения
- $D$ : входной размер
- $k$ : количество ближайших соседей
- $d$ : выходной размер
Рекомендации
- «Собственные карты Гессе: методы локально линейного вложения для многомерных данных» Донохо, Д. и Граймс, К. Proc Natl Acad Sci USA. 100: 5591 (2003)
2.2.6. Спектральное вложение
Спектральное вложение — это подход к вычислению нелинейного вложения. Scikit-learn реализует лапласианские собственные карты, которые находят низкоразмерное представление данных с использованием спектрального разложения лапласиана графа. Сгенерированный граф можно рассматривать как дискретную аппроксимацию многообразия низкой размерности в пространстве высокой размерности. Минимизация функции стоимости на основе графика гарантирует, что точки, близкие друг к другу на многообразии, отображаются близко друг к другу в низкоразмерном пространстве с сохранением локальных расстояний. Спектральное вложение может быть выполнено с помощью функции spectral_embedding или ее объектно-ориентированного аналога SpectralEmbedding.
2.2.6.1. Сложность
Алгоритм Spectral Embedding (Laplacian Eigenmaps) состоит из трех этапов:
- Построение взвешенного графа . Преобразуйте необработанные входные данные в графическое представление, используя матричное представление сходства (смежности).
- Построение графа Лапласа . ненормализованный граф Лапласиан строится как $L=D−A$ для и нормализованный как $L = D^{-\frac{1}{2}} (D — A) D^{-\frac{1}{2}}$.
- Частичное разложение на собственные значения . Разложение по собственным значениям выполняется на лапласиане графа
Общая сложность спектрального вложения составляет $O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]$.
- $N$ : количество точек данных обучения
- $D$ : входной размер
- $k$ : количество ближайших соседей
- $d$ : выходной размер
Рекомендации
- «Собственные карты Лапласа для уменьшения размерности и представления данных» М. Белкин, П. Нийоги, Нейронные вычисления, июнь 2003 г .; 15 (6): 1373-1396
2.2.7. Выравнивание местного касательного пространства
Хотя технически это не вариант LLE, локальное выравнивание касательного пространства (LTSA) алгоритмически достаточно похоже на LLE, чтобы его можно было отнести к этой категории. Вместо того, чтобы сосредотачиваться на сохранении соседних расстояний, как в LLE, LTSA стремится охарактеризовать локальную геометрию в каждой окрестности через его касательное пространство и выполняет глобальную оптимизацию для выравнивания этих локальных касательных пространств для изучения вложения. LTSA может выполняться с помощью функции locally_linear_embedding или ее объектно-ориентированного аналога LocallyLinearEmbedding с ключевым словом method = 'ltsa'.
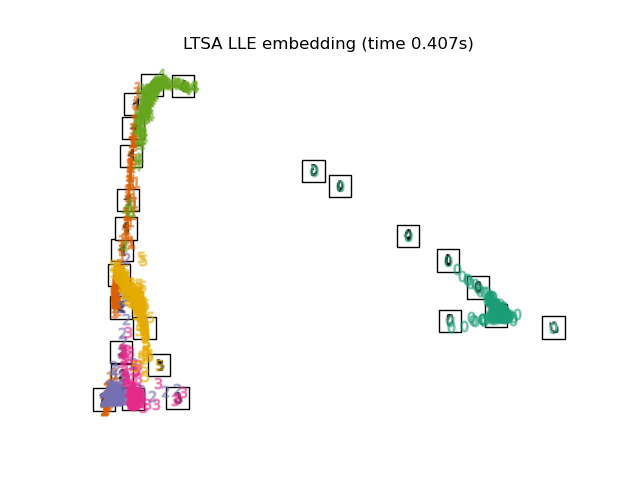
2.2.7.1. Сложност
Алгоритм LTSA состоит из трех этапов:
- Поиск ближайших соседей . То же, что и стандартный LLE
- Построение весовой матрицы . Примерно $O[D N k^3] + O[k^2 d]$. Первый член отражает стоимость, аналогичную стоимости стандартного LLE.
- Частичное разложение на собственные значения . То же, что и стандартный LLE
Общая сложность стандартного LTSA составляет $O[D \log(k) N \log(N)] + O[D N k^3] + O[k^2 d] + O[d N^2]$.
- $N$ : количество точек данных обучения
- $D$ : входной размер
- $k$ : количество ближайших соседей
- $d$ : выходной размер
Рекомендации
- «Главные многообразия и уменьшение нелинейной размерности через выравнивание касательного пространства» Чжан З. и Чжа Х. Журнал Шанхайского унив. 8: 406 (2004)
2.2.8. Многомерное масштабирование (MDS)
Многомерное масштабирование (MDS) ищет низкоразмерное представление данных, в котором расстояния хорошо соответствуют расстояниям в исходном многомерном пространстве.
В общем, MDS это метод, используемый для анализа данных о сходстве или несходстве. Он пытается смоделировать данные сходства или несходства как расстояния в геометрических пространствах. Данные могут быть рейтингами сходства между объектами, частотами взаимодействия молекул или торговыми индексами между странами.
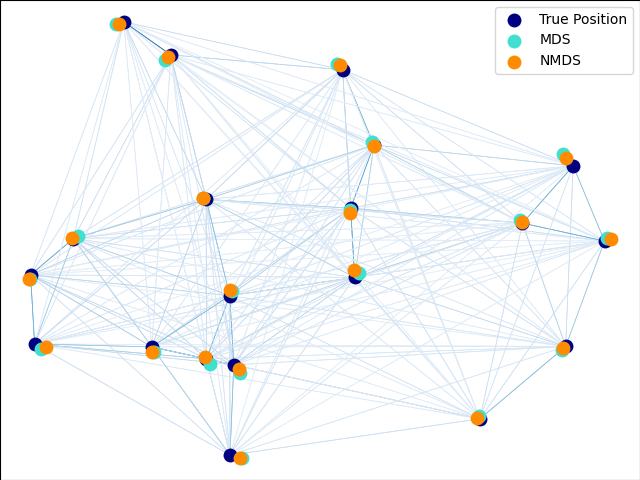
Существует два типа алгоритма MDS: метрический и неметрический. В scikit-learn класс MDS реализует оба. В Metric MDS входная матрица подобия возникает из метрики (и, таким образом, соблюдается треугольное неравенство), расстояния между двумя выходными точками затем устанавливаются как можно ближе к данным подобия или несходства. В неметрической версии алгоритмы будут пытаться сохранить порядок расстояний и, следовательно, искать монотонную связь между расстояниями во вложенном пространстве и сходствами / различиями.

Позволять $S$ — матрица подобия, а $X$ координаты nточки ввода. Несоответствия $\hat{d}_{ij}$ являются преобразованием подобранных оптимальным образом подобранных способов. Тогда цель, называемая напряжением, определяется следующим образом:
$\sum_{i < j} d_{ij}(X) — \hat{d}_{ij}(X)$
2.2.8.1. Метрические MDS
Простейшая метрическая MDS модель, называемая абсолютным MDS , различия определяются следующим образом : $\hat{d}{ij} = S{ij}$. При абсолютном MDS значение $S_{ij}$ тогда должно точно соответствовать расстоянию между точками $i$ а также $j$ в точке вложения.
Чаще всего устанавливается неравенство $\hat{d}{ij} = b S{ij}$.
2.2.8.2. Неметрические МДС
Неметрическая система MDS ориентирована на упорядочение данных. Если $S_{ij} < S_{jk}$, то вложение должно обеспечивать $d_{ij} <d_{jk}$. Простой алгоритм для обеспечения этого заключается в использовании монотонной регрессии $d_{ij}$ на $S_{ij}$, приводя к диспропорциям $\hat{d}_{ij}$ в том же порядке, что и $S_{ij}$.
Тривиальное решение этой проблемы — установить все точки в начале координат. Чтобы этого избежать, неравенство $\hat{d}_{ij}$ нормализованы.
Рекомендации
- «Современное многомерное масштабирование — теория и приложения» Борг, И .; Серия Groenen P. Springer в статистике (1997)
- «Неметрическое многомерное масштабирование: численный метод» Kruskal, J. Psychometrika, 29 (1964)
- «Многомерное масштабирование путем оптимизации соответствия неметрической гипотезе» Kruskal, J. Psychometrika, 29, (1964)
2.2.9. t-распределенное стохастическое соседнее вложение (t-SNE)
t-SNE ( TSNE) преобразует сродства точек данных в вероятности. Сходства в исходном пространстве представлены гауссовскими совместными вероятностями, а сродства во вложенном пространстве представлены t-распределениями Стьюдента. Это позволяет t-SNE быть особенно чувствительным к локальной структуре и имеет несколько других преимуществ по сравнению с существующими методами:
- Выявление структуры в разных масштабах на одной карте
- Выявление данных, которые лежат в нескольких разных коллекциях или кластерах
- Снижение тенденции к скоплению точек вместе в центре
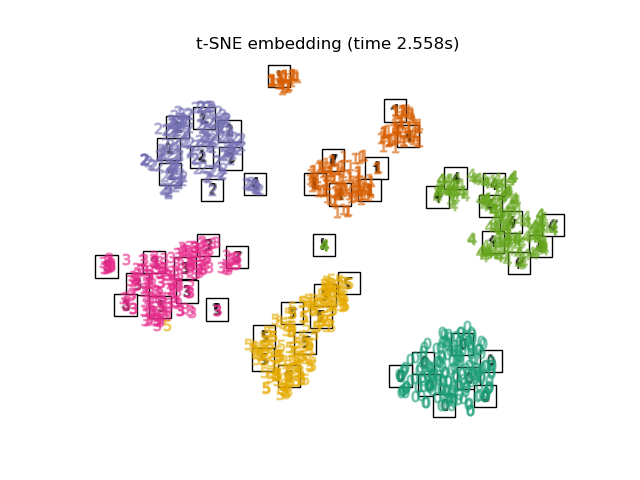
В то время как Isomap, LLE и варианты лучше всего подходят для развертывания единого непрерывного низкоразмерного многообразия, t-SNE будет фокусироваться на локальной структуре данных и будет стремиться извлекать кластерные локальные группы выборок, как показано на примере S-кривой. Эта способность группировать выборки на основе локальной структуры может быть полезной для визуального разделения набора данных, который включает сразу несколько коллекторов, как в случае набора данных цифр.
Дивергенция Кульбака-Лейблера (KL) совместных вероятностей в исходном пространстве и вложенном пространстве будет минимизирована градиентным спуском. Обратите внимание, что дивергенция KL не является выпуклой, т.е. несколько перезапусков с разными инициализациями закончатся локальными минимумами дивергенции KL. Следовательно, иногда полезно попробовать разные начальные числа и выбрать вложение с наименьшим расхождением KL.
К недостаткам использования t-SNE можно отнести примерно следующие:
- t-SNE требует больших вычислительных ресурсов и может занять несколько часов на наборах данных с миллионами выборок, тогда как PCA завершится за секунды или минуты.
- Метод t-SNE Барнса-Хата ограничен двумерным или трехмерным вложением.
- Алгоритм является стохастическим, и несколько перезапусков с разными начальными числами могут дать разные вложения. Однако вполне законно выбрать встраивание с наименьшей ошибкой.
- Глобальная структура явно не сохраняется. Эта проблема смягчается за счет инициализации точек с помощью PCA (с использованием
init='pca').
2.2.9.1. Оптимизация t-SNE
Основная цель t-SNE — визуализация данных большой размерности. Следовательно, лучше всего работает, когда данные будут встраиваться в двух или трех измерениях.
Оптимизация расхождения KL иногда может быть немного сложной. Есть пять параметров, которые контролируют оптимизацию t-SNE и, следовательно, возможно качество результирующего встраивания:
- недоумение
- фактор раннего преувеличения
- скорость обучения
- максимальное количество итераций
- угол (не используется в точном методе)
Недоумение определяется как $k=2^{(S)}$ где $S$ — энтропия Шеннона условного распределения вероятностей. Недоумение $k$-сторонний штамп $k$, чтобы $k$ фактически является числом ближайших соседей, которое t-SNE учитывает при генерации условных вероятностей. Большие сложности приводят к большему количеству ближайших соседей и менее чувствительны к мелким строениям. И наоборот, при меньшем недоумении учитывается меньшее количество соседей и, таким образом, игнорируется более глобальная информация в пользу местного соседства. По мере увеличения размеров набора данных потребуется больше точек, чтобы получить разумную выборку местного соседства, и, следовательно, могут потребоваться большие затруднения. Точно так же более зашумленные наборы данных потребуют больших значений недоумения, чтобы охватить достаточно локальных соседей, чтобы видеть за пределами фонового шума.
Максимальное количество итераций обычно достаточно велико и не требует настройки. Оптимизация состоит из двух этапов: этапа раннего преувеличения и заключительной оптимизации. Во время раннего преувеличения совместные вероятности в исходном пространстве будут искусственно увеличены путем умножения на заданный коэффициент. Более высокие факторы приводят к большим разрывам между естественными кластерами в данных. Если коэффициент слишком высок, расхождение KL может увеличиться на этом этапе. Обычно его не нужно настраивать. Критическим параметром является скорость обучения. Если он слишком низкий, градиентный спуск застрянет в плохом локальном минимуме. Если оно слишком велико, дивергенция KL увеличится во время оптимизации. Дополнительные советы можно найти в FAQ Лоренса ван дер Маатена (см. Ссылки). Последний параметр, угол, представляет собой компромисс между производительностью и точностью.Большие углы означают, что мы можем аппроксимировать большие области одной точкой, что приводит к более высокой скорости, но менее точным результатам.
«Как использовать t-SNE эффективно» дает хорошее обсуждение эффектов различных параметров, а также интерактивные графики для изучения эффектов различных параметров.
2.2.9.2. Barnes-Hut t-SNE
Реализованный здесь t-SNE Barnes-Hut обычно намного медленнее, чем другие алгоритмы обучения многообразию. Оптимизация довольно сложна, и вычисление градиента требует $O[d N log(N)]$, где $d$ количество выходных размеров и $N$ количество образцов. Метод Барнса-Хата улучшает точный метод, в котором сложность t-SNE равна $O[d N^2]$, но имеет несколько других заметных отличий:
- Реализация Barnes-Hut работает только тогда, когда целевая размерность равна 3 или меньше. 2D-случай типичен при построении визуализаций.
- Barnes-Hut работает только с плотными входными данными. Матрицы разреженных данных могут быть встроены только с помощью точного метода или могут быть аппроксимированы плотной проекцией низкого ранга, например, с использованием
TruncatedSVD - Barnes-Hut является приближением точного метода. Приближение параметризуется с помощью параметра угла, поэтому параметр угла не используется, если метод = «точный».
- Barnes-Hut значительно более масштабируемый. Barnes-Hut может использоваться для встраивания сотен тысяч точек данных, в то время как точный метод может обрабатывать тысячи образцов, прежде чем станет трудноразрешимым в вычислительном отношении.
Для целей визуализации (что является основным вариантом использования t-SNE) настоятельно рекомендуется использовать метод Barnes-Hut. Точный метод t-SNE полезен для проверки теоретических свойств вложения, возможно, в пространство более высокой размерности, но ограничивается небольшими наборами данных из-за вычислительных ограничений.
Также обратите внимание, что метки цифр примерно соответствуют естественной группировке, обнаруженной t-SNE, в то время как линейная 2D-проекция модели PCA дает представление, в котором области меток в значительной степени перекрываются. Это явный признак того, что эти данные могут быть хорошо разделены нелинейными методами, ориентированными на локальную структуру (например, SVM с гауссовым ядром RBF). Однако невозможность визуализировать хорошо разделенные однородно помеченные группы с t-SNE в 2D не обязательно означает, что данные не могут быть правильно классифицированы с помощью контролируемой модели. Возможно, двух измерений недостаточно для точного представления внутренней структуры данных.
Рекомендации
- «Визуализация многомерных данных с помощью t-SNE» ван дер Маатен, LJP; Хинтон, Дж. Журнал исследований в области машинного обучения (2008 г.)
- «Распределенное стохастическое соседнее вложение » ван дер Маатен, LJP
- «Ускорение t-SNE с использованием древовидных алгоритмов». LJP van der Maaten. Журнал исследований в области машинного обучения 15 (октябрь): 3221-3245, 2014.
2.2.10. Советы по практическому использованию
- Убедитесь, что для всех функций используется один и тот же масштаб. Поскольку многообразные методы обучения основаны на поиске ближайшего соседа, в противном случае алгоритм может работать плохо. См. StandardScaler для удобных способов масштабирования разнородных данных.
- Ошибка реконструкции, вычисленная каждой программой, может использоваться для выбора оптимального размера вывода. Дляd-мерное многообразие, вложенное в D-мерное пространство параметров, ошибка восстановления будет уменьшаться по мере
n_componentsувеличения доn_components == d. - Обратите внимание, что зашумленные данные могут «закоротить» коллектор, по сути действуя как мост между частями коллектора, которые в противном случае были бы хорошо разделены. Многообразное обучение на зашумленных и/или неполных данных — активная область исследований.
- Определенные входные конфигурации могут привести к сингулярным матрицам весов, например, когда более двух точек в наборе данных идентичны, или когда данные разделены на несвязанные группы. В этом случае
solver='arpack'не удастся найти пустое пространство. Самый простой способ решить эту проблему — использовать,solver='dense'который будет работать с сингулярной матрицей, хотя это может быть очень медленным в зависимости от количества входных точек. В качестве альтернативы можно попытаться понять источник сингулярности: если это связано с непересекающимися множествами,n_neighborsможет помочь увеличение . Если это связано с идентичными точками в наборе данных, удаление этих точек может помочь.
Смотрите также
Встраивание полностью случайных деревьев также может быть полезно для получения нелинейных представлений пространства признаков, также оно не снижает размерность.
