2.6. Оценка ковариации ¶
Многие статистические задачи требуют оценки ковариационной матрицы совокупности, которую можно рассматривать как оценку формы диаграммы разброса набора данных. В большинстве случаев такая оценка должна выполняться на выборке, свойства которой (размер, структура, однородность) имеют большое влияние на качество оценки. Пакет sklearn.covariance предоставляет инструменты для точной оценки ковариационной матрицы для данной популяции в различных условиях.
Мы предполагаем, что наблюдения независимы и одинаково распределены (iid).
2.6.1. Эмпирическая ковариация
Ковариационная матрица набора данных хорошо аппроксимируется классической оценкой максимального правдоподобия (или «эмпирической ковариацией») при условии, что количество наблюдений достаточно велико по сравнению с количеством признаков (переменных, описывающих наблюдения). Точнее, оценщик максимального правдоподобия выборки — это асимптотически несмещенный оценщик ковариационной матрицы соответствующей совокупности.
Эмпирическая ковариационная матрица выборки может быть вычислена с использованием empirical_covariance функции пакета или путем подгонки EmpiricalCovariance объекта к выборке данных с помощью EmpiricalCovariance.fit метода. Будьте осторожны, чтобы результаты зависели от центрирования данных, поэтому можно использовать assume_centered параметр точно. Точнее, если assume_centered=False, то предполагается, что тестовый набор имеет тот же средний вектор, что и обучающий набор. В противном случае оба должны быть центрированы пользователем и assume_centered=True использоваться.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
EmpiricalCovarianceобъект к данным.
2.6.2. Уменьшение ковариации
2.6.2.1. Базовая усадка
Несмотря на то, что он является асимптотически несмещенным оценщиком ковариационной матрицы, оценщик максимального правдоподобия не является хорошим оценщиком собственных значений ковариационной матрицы, поэтому матрица точности, полученная в результате ее обращения, не является точной. Иногда даже оказывается, что эмпирическая ковариационная матрица не может быть инвертирована по числовым причинам. Для того, чтобы избежать такой проблемы инверсии, преобразование эмпирической ковариационной матрицы было введено: shrinkage.
В scikit-learn это преобразование (с определяемым пользователем коэффициентом усадки) можно напрямую применить к предварительно вычисленной ковариации с помощью shrunk_covariance метода. Кроме того, сжатая оценка ковариации может быть адаптирована к данным с помощью ShrunkCovariance объекта и его ShrunkCovariance.fit метода. Опять же, результаты зависят от того, центрированы ли данные, поэтому можно использовать assume_centered параметр точно.
Математически это сжатие состоит в уменьшении отношения между наименьшим и наибольшим собственными значениями эмпирической ковариационной матрицы. Это можно сделать, просто сдвинув каждое собственное значение в соответствии с заданным смещением, что эквивалентно нахождению оценщика максимального правдоподобия со штрафом l2 ковариационной матрицы. На практике усадка сводится к простому выпуклому преобразованию: $\Sigma_{\rm shrunk} = (1-\alpha)\hat{\Sigma} + \alpha\frac{{\rm Tr}\hat{\Sigma}}{p}\rm Id$.
Выбирая величину усадки, $\alpha$ сводится к установлению компромисса смещения/дисперсии и обсуждается ниже.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
ShrunkCovarianceобъект к данным.
2.6.2.2. Усадка Ледуа-Вольфа
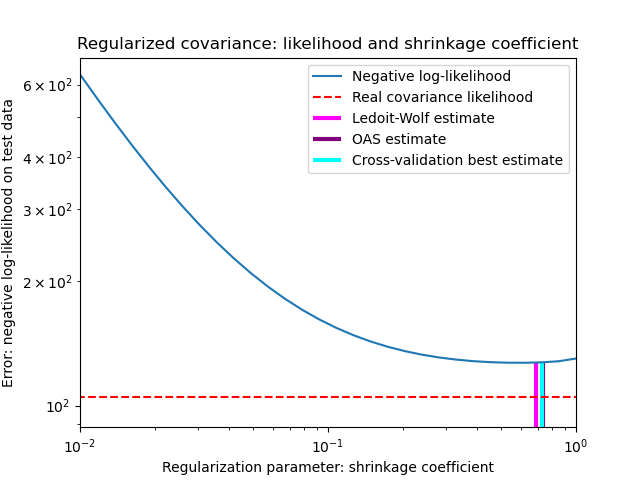
В своей статье 1 2004 г. О. Ледуа и М. Вольф предлагают формулу для расчета оптимального коэффициента усадки.α который минимизирует среднеквадратичную ошибку между оценочной и реальной ковариационной матрицей.
Оценщик Ледойта-Вольфа ковариационной матрицы может быть вычислен на выборке с ledoit_wolf функцией sklearn.covariance пакета, или ее можно получить иным способом, подгоняя LedoitWolf объект к той же выборке.
Примечание Случай, когда ковариационная матрица популяций изотропна
Важно отметить, что когда количество образцов намного превышает количество элементов, можно ожидать, что усадка не потребуется. Интуиция, лежащая в основе этого, заключается в том, что если ковариация совокупности имеет полный ранг, когда количество выборок растет, ковариация выборки также станет положительно определенной. В результате усадка не потребуется, и метод должен делать это автоматически.
Однако это не так в процедуре Ледуа-Вольфа, когда ковариация совокупности оказывается кратной единичной матрице. В этом случае оценка усадки Ледуа-Вольфа приближается к 1 по мере увеличения количества образцов. Это указывает на то, что оптимальная оценка ковариационной матрицы в смысле Ледуа-Вольфа кратна единице. Поскольку ковариация населения уже кратна единичной матрице, решение Ледуа-Вольфа действительно является разумной оценкой.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
LedoitWolfобъект к данным и визуализировать характеристики оценщика Ледуа-Вольфа с точки зрения правдоподобия.
Рекомендации
О. Ледойт и М. Вольф, «Хорошо обусловленная оценка для многомерных ковариационных матриц», Журнал многомерного анализа, том 88, выпуск 2, февраль 2004 г., страницы 365-411.
2.6.2.3. Приблизительная усадка Oracle
Предполагая, что данные распределены по Гауссу, Chen et al. 2 выведена формула, направленная на выбор коэффициента усадки, который дает меньшую среднеквадратичную ошибку, чем та, которая дается формулой Ледуа и Вольфа. Результирующая оценка известна как оценка ковариации Oracle Shrinkage Approximating.
Оценщик OAS ковариационной матрицы может быть вычислен на выборке с помощью oas функции sklearn.covariance пакета, или он может быть получен иным образом путем подгонки OAS объекта к той же выборке.
Компромисс смещения и дисперсии при установке усадки: сравнение вариантов оценок Ледуа-Вольфа и OAS
Рекомендации
Чен и др., «Алгоритмы сжатия для оценки ковариации MMSE», IEEE Trans. на знак. Proc., Volume 58, Issue 10, October 2010.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
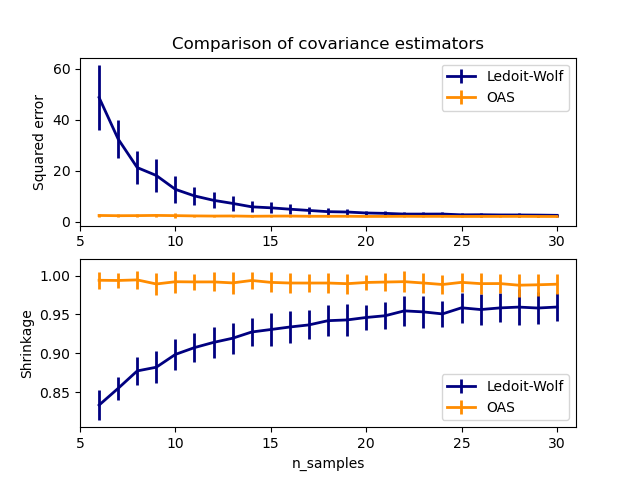
OASобъект к данным. - См. Оценку Ледуа-Вольфа и OAS для визуализации разницы среднеквадратических ошибок между a
LedoitWolfиOASоценкой ковариации.
2.6.3. Редкая обратная ковариация
Матрица, обратная ковариационной матрице, часто называемая матрицей точности, пропорциональна матрице частичной корреляции. Это дает частичную независимость отношениям. Другими словами, если два признака независимы друг от друга условно, соответствующий коэффициент в матрице точности будет равен нулю. Вот почему имеет смысл оценивать матрицу разреженной точности: оценка ковариационной матрицы лучше обусловлена изучением отношений независимости от данных. Это называется ковариационным отбором .
В ситуации с малой выборкой, в которой n_samples порядок n_features или меньше, разреженные оценки обратной ковариации, как правило, работают лучше, чем оценки сжатой ковариации. Однако в противоположной ситуации или для сильно коррелированных данных они могут быть численно нестабильными. Кроме того, в отличие от оценщиков усадки, разреженные оценщики могут восстанавливать недиагональную структуру.
Оценщик GraphicalLasso использует l1 штраф для обеспечения разреженности на высокоточной матрице: тем выше его alpha параметр, тем более разреженной прецизионную матрицу. Соответствующий GraphicalLassoCV объект использует перекрестную проверку для автоматической установки alpha параметра.
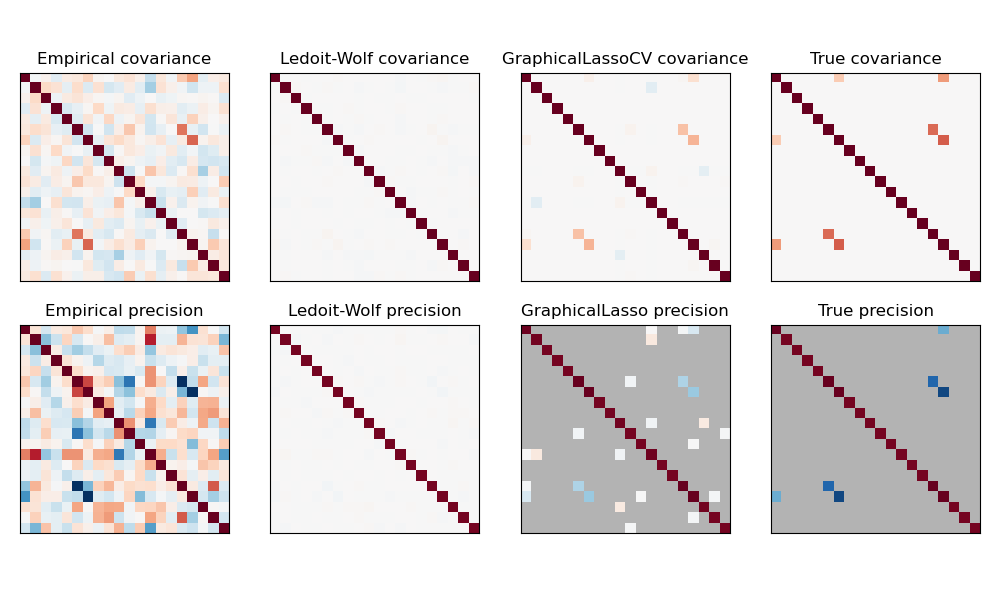
Сравнение максимального правдоподобия, усадки и разреженных оценок ковариации и матрицы точности в настройках очень малых выборок.
Примечание Восстановление структуры
Восстановление графической структуры из корреляций в данных — непростая задача. Если вы заинтересованы в таком восстановлении, имейте в виду, что:
- Восстановление легче из корреляционной матрицы, чем из ковариационной матрицы: стандартизируйте свои наблюдения перед запуском
GraphicalLasso - Если в нижележащем графе есть узлы с гораздо большим количеством соединений, чем в среднем узле, алгоритм пропустит некоторые из этих соединений.
- Если количество ваших наблюдений невелико по сравнению с количеством ребер в вашем нижележащем графе, вы не сможете его восстановить.
- Даже если вы находитесь в благоприятных условиях восстановления, альфа-параметр, выбранный путем перекрестной проверки (например, с использованием
GraphicalLassoCVобъекта), приведет к выбору слишком большого количества ребер. Однако соответствующие ребра будут иметь больший вес, чем нерелевантные.
Математическая формулировка следующая:
$$\hat{K} = \mathrm{argmin}_K \big( \mathrm{tr} S K — \mathrm{log} \mathrm{det} K + \alpha |K|_1 \big)$$
Где $K$ — матрица точности, которую необходимо оценить, и $S$ — это выборочная ковариационная матрица. $|K|_1$ — сумма модулей недиагональных коэффициентов $K$. Для решения этой проблемы используется алгоритм GLasso из статьи Friedman 2008 Biostatistics. Это тот же алгоритм, что и в glasso пакете R.
Примеры
- Оценка разреженной обратной ковариации: пример синтетических данных, показывающих восстановление структуры и сравнение с другими оценками ковариации.
- Визуализация структуры фондового рынка: пример реальных данных фондового рынка, определение наиболее связанных символов.
Рекомендации
- Фридман и др., «Оценка разреженной обратной ковариации с помощью графического лассо» , Biostatistics 9, стр. 432, 2008 г.
2.6.4. Оценка робастной ковариации
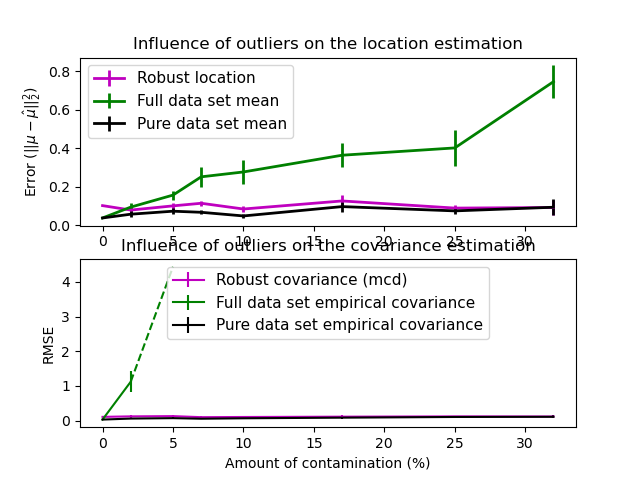
Реальные наборы данных часто подвержены ошибкам измерения или записи. Регулярные, но необычные наблюдения также могут появляться по разным причинам. Наблюдения, которые случаются очень редко, называются выбросами. Эмпирическая оценка ковариации и сжатая оценка ковариации, представленные выше, очень чувствительны к наличию выбросов в данных. Следовательно, следует использовать надежные оценщики ковариации для оценки ковариации реальных наборов данных. В качестве альтернативы можно использовать робастные оценщики ковариации для обнаружения выбросов и отбрасывания / уменьшения веса некоторых наблюдений в соответствии с дальнейшей обработкой данных.
В sklearn.covariance пакете реализована надежная оценка ковариации, определитель минимальной ковариации 3 .
2.6.4.1. Определитель минимальной ковариации
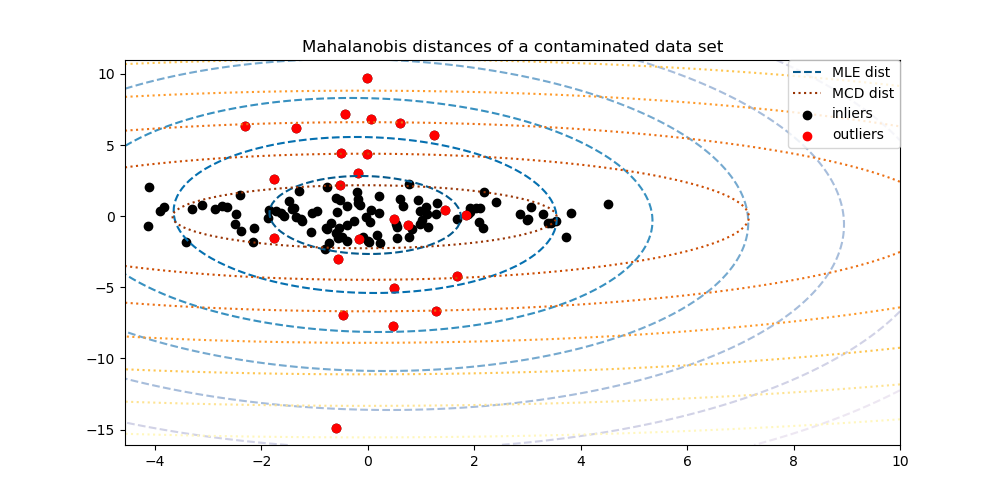
Оценщик, определяющий минимальную ковариацию, — это надежный оценщик ковариации набора данных, представленный PJ Rousseeuw в 3 . Идея состоит в том, чтобы найти заданную пропорцию (h) «хороших» наблюдений, которые не являются выбросами, и вычислить их эмпирическую ковариационную матрицу. Эта эмпирическая ковариационная матрица затем масштабируется, чтобы компенсировать выполненный выбор наблюдений («этап согласованности»). Вычислив оценку определителя минимальной ковариации, можно присвоить веса наблюдениям в соответствии с их расстоянием Махаланобиса, что приведет к повторной оценке ковариационной матрицы набора данных («этап повторного взвешивания»).
Rousseeuw и Van Driessen 4 разработали алгоритм FastMCD для вычисления определителя минимальной ковариации. Этот алгоритм используется в scikit-learn при подгонке объекта MCD к данным. Алгоритм FastMCD также одновременно вычисляет надежную оценку местоположения набора данных.
Сырые оценки могут быть доступны как raw_location_ и raw_covariance_ атрибутами из MinCovDet надежного объекта ковариационной оценивани.
Рекомендации
- 3 PJ Rousseeuw. Наименьшая медиана квадратов регрессии. Дж. Ам Стат Асс, 79: 871, 1984.
- 4 Быстрый алгоритм для определения определителя минимальной ковариации, 1999, Американская статистическая ассоциация и Американское общество качества, TECHNOMETRICS.
Примеры
- См. Пример надежной и эмпирической ковариационной оценки, чтобы узнать, как подогнать
MinCovDetобъект к данным, и посмотрите, насколько оценка остается точной, несмотря на наличие выбросов. - См оценку ковариационной Robust и Махаланобиса расстояния Актуальность визуализировать разницу между
EmpiricalCovarianceиMinCovDetковариации оценок с точки зрения расстояния Махаланобиса (так мы получим более точную оценку точности матрицы тоже).