3.4. Кривые валидации: построение оценок для оценки моделей ¶
У каждого оценщика есть свои достоинства и недостатки. Его ошибку обобщения можно разложить на смещение, дисперсию и шум. Смещения из оценки является его средней ошибкой для различных наборов обучения. Дисперсия из оценки указывает на то, насколько чувствительна она к различным наборы обучения. Шум — это свойство данных.
На следующем графике мы видим функцию $f(x) = \cos (\frac{3}{2} \pi x)$ и несколько шумных сэмплов из этой функции. Мы используем три различных оценщика для подбора функции: линейная регрессия с полиномиальными признаками степени 1, 4 и 15. Мы видим, что первая оценка может в лучшем случае обеспечить только плохое соответствие выборкам и истинную функцию, потому что она слишком проста ( высокое смещение), второй оценщик аппроксимирует его почти идеально, а последний оценщик идеально аппроксимирует обучающие данные, но не очень хорошо соответствует истинной функции, т.е. он очень чувствителен к изменяющимся обучающим данным (высокая дисперсия).
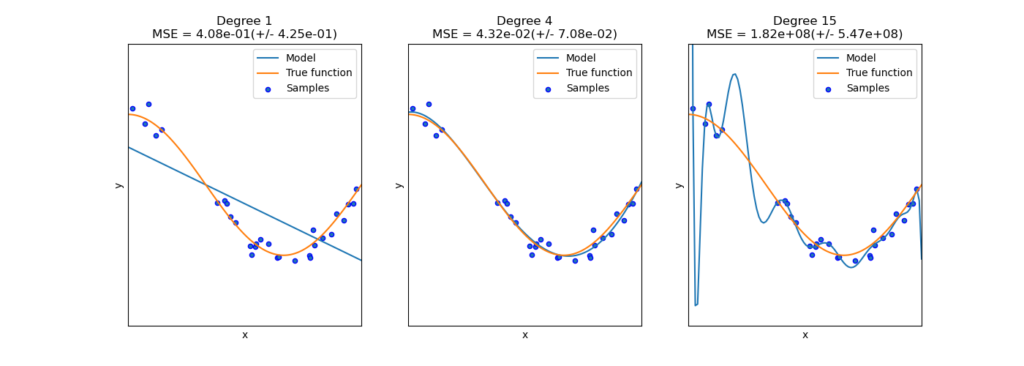
Смещение и дисперсия являются неотъемлемыми свойствами оценщиков, и обычно нам приходится выбирать алгоритмы обучения и гиперпараметры так, чтобы смещение и дисперсия были как можно более низкими (см. Дилемма смещения и дисперсии ). Еще один способ уменьшить дисперсию модели — использовать больше обучающих данных. Однако вам следует собирать больше обучающих данных только в том случае, если истинная функция слишком сложна для аппроксимации с помощью оценщика с более низкой дисперсией.
В простой одномерной задаче, которую мы видели в примере, легко увидеть, страдает ли оценка от смещения или дисперсии. Однако в многомерных пространствах модели могут стать очень трудными для визуализации. По этой причине часто бывает полезно использовать инструменты, описанные ниже.
Примеры:
3.4.1. Кривая валидации
Для проверки модели нам нужна функция оценки (см. « Метрики и оценка: количественная оценка качества прогнозов» ), например, точность для классификаторов. Правильный способ выбора нескольких гиперпараметров оценщика — это, конечно, поиск по сетке или аналогичные методы (см. Настройка гиперпараметров оценщика ), которые выбирают гиперпараметр с максимальной оценкой в наборе проверки или нескольких наборах проверки. Обратите внимание, что если мы оптимизировали гиперпараметры на основе оценки валидации, оценка валидации будет смещена и больше не будет хорошей оценкой обобщения. Чтобы получить правильную оценку обобщения, мы должны вычислить оценку на другом наборе тестов.
Однако иногда полезно построить график влияния одного гиперпараметра на оценку обучения и оценку валидации, чтобы выяснить, соответствует ли оценка некоторым значениям гиперпараметров.
Функция validation_curve может помочь в этом случае:
>>> import numpy as np
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import Ridge
>>> np.random.seed(0)
>>> X, y = load_iris(return_X_y=True)
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]
>>> train_scores, valid_scores = validation_curve(Ridge(), X, y, "alpha",
... np.logspace(-7, 3, 3),
... cv=5)
>>> train_scores
array([[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.51..., 0.52..., 0.49..., 0.47..., 0.49...]])
>>> valid_scores
array([[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.46..., 0.25..., 0.50..., 0.49..., 0.52...]])Если и оценка обучения, и оценка валидации низкие, оценщик не соответствует требованиям. Если оценка обучения высока, а оценка валидации низка, оценщик переобучен, а в противном случае он работает очень хорошо. Низкая оценка обучения и высокая оценка валидации обычно невозможны. Недостаток, переоснащение и рабочая модель показаны на графике ниже, где мы меняем параметр $\gamma$ SVM в наборе данных цифр.
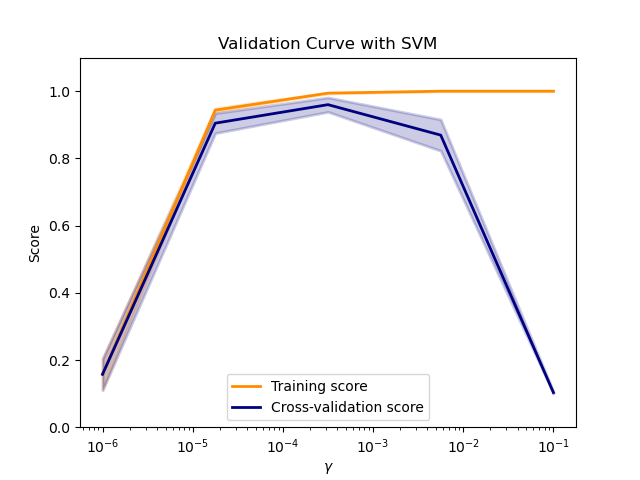
3.4.2. Кривая обучения
Кривая обучения показывает оценку валидации и обучения оценщика для различного количества обучающих выборок. Это инструмент, позволяющий узнать, насколько мы выигрываем от добавления дополнительных обучающих данных и страдает ли оценщик больше от ошибки дисперсии или ошибки смещения. Рассмотрим следующий пример, где мы строим кривую обучения наивного байесовского классификатора и SVM.
Для наивного Байеса и оценка валидации, и оценка обучения сходятся к значению, которое является довольно низким с увеличением размера обучающей выборки. Таким образом, мы, вероятно, не выиграем от большего количества обучающих данных.
Напротив, для небольших объемов данных оценка обучения SVM намного больше, чем оценка валидации. Добавление большего количества обучающих выборок, скорее всего, усилит обобщение.
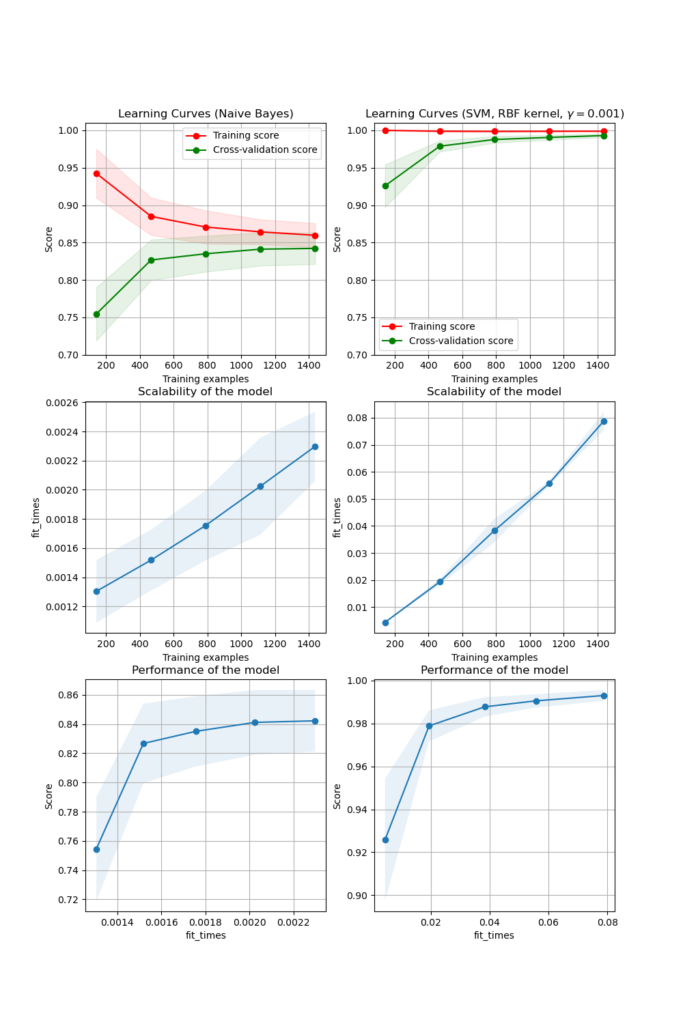
Мы можем использовать эту функцию learning_curve для генерации значений, необходимых для построения такой кривой обучения (количество использованных выборок, средние оценки на обучающих наборах и средние баллы на проверочных наборах):
>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC
>>> train_sizes, train_scores, valid_scores = learning_curve(
... SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes
array([ 50, 80, 110])
>>> train_scores
array([[0.98..., 0.98 , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.99...]])
>>> valid_scores
array([[1. , 0.93..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...]])