6.3. Предварительная обработка данных ¶

Пакет sklearn.preprocessing обеспечивает несколько функций общей полезности и трансформаторные классы для изменения необработанных векторов характеристик в представление , которое является более подходящим для нисходящих потока оценок.

В целом алгоритмы обучения выигрывают от стандартизации набора данных. Если в наборе присутствуют какие-то выбросы, более подходящими являются надежные скейлеры или трансформаторы. Поведение различных средств масштабирования, преобразователей и нормализаторов в наборе данных, содержащем предельные выбросы, выделено в разделе «Сравнить влияние различных средств масштабирования на данные с выбросами» .

6.3.1. Стандартизация или удаление среднего и масштабирование дисперсии

Стандартизация наборов данных является общим требованием для многих оценщиков машинного обучения, реализованных в scikit-learn; они могут вести себя плохо, если отдельные функции не более или менее выглядят как стандартные нормально распределенные данные: гауссовские с нулевым средним и единичной дисперсией .

На практике мы часто игнорируем форму распределения и просто преобразуем данные для их центрирования, удаляя среднее значение каждой функции, а затем масштабируем ее, деля непостоянные характеристики на их стандартное отклонение.

Например, многие элементы, используемые в целевой функции алгоритма обучения (такие как ядро ​​RBF машин опорных векторов или регуляризаторы l1 и l2 линейных моделей), предполагают, что все функции сосредоточены вокруг нуля и имеют дисперсию в том же порядке. Если характеристика имеет дисперсию, которая на порядки больше, чем у других, она может доминировать над целевой функцией и сделать оценщик неспособным правильно учиться на других функциях, как ожидалось.

Модуль preprocessing предоставляет StandardScaler вспомогательный класс, который является быстрым и простым способом , чтобы выполнить следующую операцию на массив-типа набора данных:

>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> scaler
StandardScaler()

>>> scaler.mean_
array([1. ..., 0. ..., 0.33...])

>>> scaler.scale_
array([0.81..., 0.81..., 1.24...])

>>> X_scaled = scaler.transform(X_train)
>>> X_scaled
array([[ 0.  ..., -1.22...,  1.33...],
       [ 1.22...,  0.  ..., -0.26...],
       [-1.22...,  1.22..., -1.06...]])

Масштабированные данные имеют нулевое среднее значение и единичную дисперсию:

>>> X_scaled.mean(axis=0)
array([0., 0., 0.])

>>> X_scaled.std(axis=0)
array([1., 1., 1.])

Этот класс реализует Transformer API для вычисления среднего и стандартного отклонения на обучающем наборе, чтобы иметь возможность позже повторно применить то же преобразование к набору тестирования. Таким образом, этот класс подходит для использования на ранних этапах Pipeline:

>>> from sklearn.datasets import make_classification
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler

>>> X, y = make_classification(random_state=42)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
>>> pipe = make_pipeline(StandardScaler(), LogisticRegression())
>>> pipe.fit(X_train, y_train)  # apply scaling on training data
Pipeline(steps=[('standardscaler', StandardScaler()),
                ('logisticregression', LogisticRegression())])

>>> pipe.score(X_test, y_test)  # apply scaling on testing data, without leaking training data.
0.96

Можно отключить центрирование или масштабирование, передав with_mean=False или with_std=False в конструктор StandardScaler.

6.3.1.1. Масштабирование функций до диапазона

Альтернативная стандартизация — это масштабирование функций таким образом, чтобы они находились между заданным минимальным и максимальным значением, часто между нулем и единицей, или так, чтобы максимальное абсолютное значение каждой функции масштабировалось до размера единицы. Этого можно добиться с помощью MinMaxScaler или MaxAbsScaler соответственно.

Мотивация к использованию этого масштабирования включает устойчивость к очень небольшим стандартным отклонениям функций и сохранение нулевых записей в разреженных данных.

Вот пример масштабирования матрицы данных игрушки до диапазона [0, 1]:

>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
...
>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> X_train_minmax = min_max_scaler.fit_transform(X_train)
>>> X_train_minmax
array([[0.5       , 0.        , 1.        ],
       [1.        , 0.5       , 0.33333333],
       [0.        , 1.        , 0.        ]])

Тот же экземпляр преобразователя затем можно применить к некоторым новым тестовым данным, невидимым во время вызова подгонки: будут применены те же операции масштабирования и сдвига, чтобы они согласовывались с преобразованием, выполняемым с данными поезда:

>>> X_test = np.array([[-3., -1.,  4.]])
>>> X_test_minmax = min_max_scaler.transform(X_test)
>>> X_test_minmax
array([[-1.5       ,  0.        ,  1.66666667]])

Можно проанализировать атрибуты масштабатора, чтобы узнать точную природу преобразования, полученного на обучающих данных:

>>> min_max_scaler.scale_
array([0.5       , 0.5       , 0.33...])

>>> min_max_scaler.min_
array([0.        , 0.5       , 0.33...])

Если MinMaxScaler дано явное указание, полная формула будет иметь следующий вид : feature_range=(min, max)

X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))

X_scaled = X_std * (max - min) + min

MaxAbsScaler работает очень похожим образом, но масштабируется таким образом, что обучающие данные лежат в пределах диапазона [-1, 1], путем деления на наибольшее максимальное значение в каждой функции. Он предназначен для данных, которые уже сосредоточены на нуле или разреженных данных.

Вот как использовать данные игрушки из предыдущего примера с этим скейлером:

>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
...
>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> X_train_maxabs = max_abs_scaler.fit_transform(X_train)
>>> X_train_maxabs
array([[ 0.5, -1. ,  1. ],
       [ 1. ,  0. ,  0. ],
       [ 0. ,  1. , -0.5]])
>>> X_test = np.array([[ -3., -1.,  4.]])
>>> X_test_maxabs = max_abs_scaler.transform(X_test)
>>> X_test_maxabs
array([[-1.5, -1. ,  2. ]])
>>> max_abs_scaler.scale_
array([2.,  1.,  2.])

6.3.1.2. Масштабирование разреженных данных

Центрирование разреженных данных разрушило бы структуру разреженности данных, и поэтому редко бывает разумным делом. Однако может иметь смысл масштабировать разреженные входные данные, особенно если функции находятся в разных масштабах.

MaxAbsScaler был специально разработан для масштабирования разреженных данных, и это рекомендуемый способ сделать это. Однако StandardScaler может принимать scipy.sparse матрицы в качестве входных данных, если with_mean=False явно передается в конструктор. В противном случае ValueErrorбудет поднят a , поскольку тихое центрирование нарушит разреженность и часто приведет к сбою выполнения из-за непреднамеренного выделения чрезмерного количества памяти. RobustScaler не может быть приспособлен к разреженным входам, но вы можете использовать этот transform метод для разреженных входных данных.

Обратите внимание, что средства масштабирования принимают форматы сжатых разреженных строк и сжатых разреженных столбцов (см. scipy.sparse.csr_matrix и scipy.sparse.csc_matrix). Любой другой разреженный ввод будет преобразован в представление сжатых разреженных строк . Чтобы избежать ненужных копий памяти, рекомендуется выбирать восходящее представление CSR или CSC.

Наконец, если ожидается, что центрированные данные будут достаточно маленькими, toarrayеще один вариант — явное преобразование входных данных в массив с использованием метода разреженных матриц.

6.3.1.3. Масштабирование данных с помощью выбросов

Если ваши данные содержат много выбросов, масштабирование с использованием среднего значения и дисперсии данных, вероятно, не будет работать очень хорошо. В этих случаях вы можете использовать RobustScaler вместо него замену. Он использует более надежные оценки для центра и диапазона ваших данных.

6.3.1.4. Центрирование ядерных матриц

Если у вас есть матрица ядра ядра $K$ который вычисляет скалярное произведение в пространстве функций, определяемом функцией $\phi$, a KernelCenterer может преобразовать матрицу ядра так, чтобы она содержала внутренние продукты в пространстве функций, определяемом $\phi$ с последующим удалением среднего в этом пространстве.

6.3.2. Нелинейное преобразование

Доступны два типа преобразований: квантильные преобразования и степенные преобразования. И квантильные, и степенные преобразования основаны на монотонных преобразованиях характеристик и, таким образом, сохраняют ранг значений по каждой характеристике.

Квантильные преобразования помещают все функции в одно и то же желаемое распределение на основе формулы $G^{-1}(F(X))$ где $F$ — кумулятивная функция распределения признака и $G^{-1}$ функция квантиля требуемого распределения выходного $G$. В этой формуле используются два следующих факта: (i) если $X$ случайная величина с непрерывной кумулятивной функцией распределения $F$ тогда $F(X)$ равномерно распределяется по [0,1]; (ii) еслиU — случайная величина с равномерным распределением на $[0,1]$ тогда $G^{−1}(U)$ имеет распространение $G$. Выполняя ранговое преобразование, квантильное преобразование сглаживает необычные распределения и меньше подвержено влиянию выбросов, чем методы масштабирования. Однако это искажает корреляции и расстояния внутри и между объектами.

Преобразования мощности — это семейство параметрических преобразований, цель которых — сопоставить данные из любого распределения как можно ближе к гауссовскому распределению.

6.3.2.1. Отображение в равномерное распределение

QuantileTransformer обеспечивает непараметрическое преобразование для отображения данных в равномерное распределение со значениями от 0 до 1:

>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
>>> quantile_transformer = preprocessing.QuantileTransformer(random_state=0)
>>> X_train_trans = quantile_transformer.fit_transform(X_train)
>>> X_test_trans = quantile_transformer.transform(X_test)
>>> np.percentile(X_train[:, 0], [0, 25, 50, 75, 100]) 
array([ 4.3,  5.1,  5.8,  6.5,  7.9])

Эта особенность соответствует длине чашелистиков в см. После применения квантильного преобразования эти ориентиры близко подходят к ранее определенным процентилям:

>>> np.percentile(X_train_trans[:, 0], [0, 25, 50, 75, 100])
... 
array([ 0.00... ,  0.24...,  0.49...,  0.73...,  0.99... ])

Это можно подтвердить на независимом тестовом наборе с аналогичными замечаниями:

>>> np.percentile(X_test[:, 0], [0, 25, 50, 75, 100])
... 
array([ 4.4  ,  5.125,  5.75 ,  6.175,  7.3  ])
>>> np.percentile(X_test_trans[:, 0], [0, 25, 50, 75, 100])
... 
array([ 0.01...,  0.25...,  0.46...,  0.60... ,  0.94...])

6.3.2.2. Отображение в гауссово распределение

Во многих сценариях моделирования желательна нормальность функций в наборе данных. Преобразования мощности — это семейство параметрических монотонных преобразований, которые нацелены на отображение данных из любого распределения как можно ближе к гауссовскому распределению, чтобы стабилизировать дисперсию и минимизировать асимметрию.

PowerTransformer в настоящее время предоставляет два таких преобразования мощности, преобразование Йео-Джонсона и преобразование Бокса-Кокса.

Преобразование Йео-Джонсона определяется следующим образом:

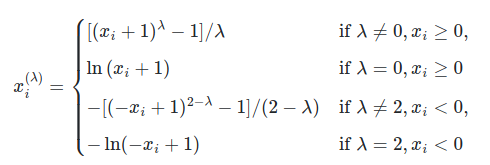
в то время как преобразование Бокса-Кокса задается следующим образом:

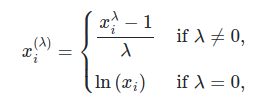
Бокс-Кокса можно применять только к строго положительным данным. В обоих методах преобразование параметризуется $\lampda$, который определяется путем оценки максимального правдоподобия. Вот пример использования Box-Cox для сопоставления выборок, взятых из логнормального распределения, в нормальное распределение:

>>> pt = preprocessing.PowerTransformer(method='box-cox', standardize=False)
>>> X_lognormal = np.random.RandomState(616).lognormal(size=(3, 3))
>>> X_lognormal
array([[1.28..., 1.18..., 0.84...],
       [0.94..., 1.60..., 0.38...],
       [1.35..., 0.21..., 1.09...]])
>>> pt.fit_transform(X_lognormal)
array([[ 0.49...,  0.17..., -0.15...],
       [-0.05...,  0.58..., -0.57...],
       [ 0.69..., -0.84...,  0.10...]])

Хотя в приведенном выше примере standardize параметр установлен на False, PowerTransformer по умолчанию будет применяться нормализация с нулевым средним и единичной дисперсией к преобразованному результату.

Ниже приведены примеры Бокса-Кокса и Йео-Джонсона, примененные к различным распределениям вероятностей. Обратите внимание, что при применении к определенным распределениям степенные преобразования достигают результатов, очень похожих на гауссову, но с другими они неэффективны. Это подчеркивает важность визуализации данных до и после преобразования.

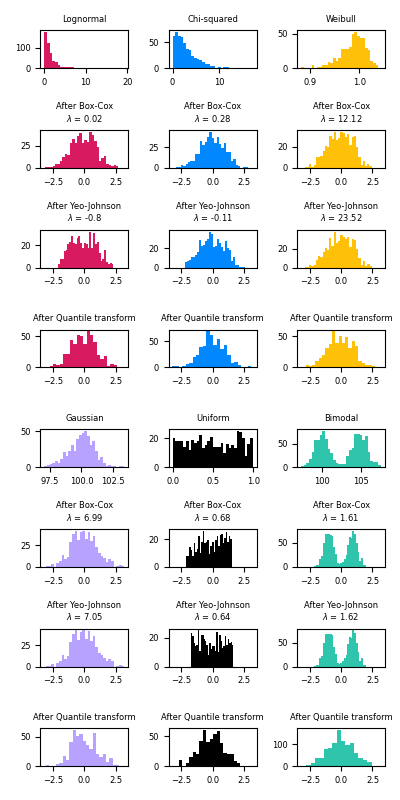
Также можно сопоставить данные с нормальным распределением, используя QuantileTransformer настройку output_distribution='normal'. Используя предыдущий пример с набором данных радужной оболочки:

>>> quantile_transformer = preprocessing.QuantileTransformer(
...     output_distribution='normal', random_state=0)
>>> X_trans = quantile_transformer.fit_transform(X)
>>> quantile_transformer.quantiles_
array([[4.3, 2. , 1. , 0.1],
       [4.4, 2.2, 1.1, 0.1],
       [4.4, 2.2, 1.2, 0.1],
       ...,
       [7.7, 4.1, 6.7, 2.5],
       [7.7, 4.2, 6.7, 2.5],
       [7.9, 4.4, 6.9, 2.5]])

Таким образом, медиана входа становится средним значением выхода с центром в 0. Нормальный выход обрезается так, чтобы минимум и максимум входа — соответствующие квантилям 1e-7 и 1 — 1e-7 соответственно — не становились бесконечными при преобразование.

6.3.3. Нормализация

Нормализация — это процесс масштабирования отдельных образцов до единичной нормы . Этот процесс может быть полезен, если вы планируете использовать квадратичную форму, такую ​​как скалярное произведение или любое другое ядро, для количественной оценки подобия любой пары образцов.

Это предположение является основой модели векторного пространства, часто используемой в контекстах классификации и кластеризации текста.

Функция normalize обеспечивает быстрый и простой способ для выполнения этой операции на одном массиве, как набор данных, либо с помощью l1, l2или max нормы:

>>> X = [[ 1., -1.,  2.],
...      [ 2.,  0.,  0.],
...      [ 0.,  1., -1.]]
>>> X_normalized = preprocessing.normalize(X, norm='l2')

>>> X_normalized
array([[ 0.40..., -0.40...,  0.81...],
       [ 1.  ...,  0.  ...,  0.  ...],
       [ 0.  ...,  0.70..., -0.70...]])

preprocessingМодуль дополнительно содержит вспомогательный класс , Normalizer который реализует ту же самую операцию с использованием TransformerAPI (даже если fit метод бесполезен в этом случае: класс является лицом без этой операции , как трактует образцов независимо друг от друга).

Таким образом, этот класс подходит для использования на ранних этапах Pipeline:

>>> normalizer = preprocessing.Normalizer().fit(X)  # fit does nothing
>>> normalizer
Normalizer()

Экземпляр нормализатора затем можно использовать в векторах выборки как любой преобразователь:

>>> normalizer.transform(X)
array([[ 0.40..., -0.40...,  0.81...],
       [ 1.  ...,  0.  ...,  0.  ...],
       [ 0.  ...,  0.70..., -0.70...]])

>>> normalizer.transform([[-1.,  1., 0.]])
array([[-0.70...,  0.70...,  0.  ...]])

Примечание. Нормализация L2 также известна как предварительная обработка пространственных знаков.

6.3.4. Кодирование категориальных признаков

Часто характеристики задаются не как непрерывные значения, а как категориальные. Например, человек может иметь функции [«male», «female»][«from Europe», «from US», «from Asia»], [«uses Firefox», «uses Chrome», «uses Safari», «uses Internet Explorer»]. Такие функции могут быть эффективно закодированы как целые числа, например [«male», «from US», «uses Internet Explorer»], может быть выражена как [0, 1, 3] в то время как [«female», «from Asia», «uses Chrome»] было бы [1, 2, 1].

Чтобы преобразовать категориальные признаки в такие целочисленные коды, мы можем использовать расширение OrdinalEncoder. Этот оценщик преобразует каждую категориальную характеристику в одну новую характеристику целых чисел (от 0 до n_categories — 1):

>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OrdinalEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari']])
array([[0., 1., 1.]])

Такое целочисленное представление, однако, не может использоваться напрямую со всеми оценщиками scikit-learn, поскольку они ожидают непрерывного ввода и интерпретируют категории как упорядоченные, что часто нежелательно (т. Е. Набор браузеров был упорядочен произвольно).

Еще одна возможность преобразовать категориальные функции в функции, которые можно использовать с оценками scikit-learn, — это использовать кодировку «один из K», также известную как одноразовое или фиктивное кодирование. Этот тип кодирования может быть получен с помощью OneHotEncoder, который преобразует каждый категориальный признак с n_categories возможными значениями в n_categories двоичные признаки, один из которых равен 1, а все остальные 0.

Продолжая пример выше:

>>> enc = preprocessing.OneHotEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari'],
...                ['male', 'from Europe', 'uses Safari']]).toarray()
array([[1., 0., 0., 1., 0., 1.],
       [0., 1., 1., 0., 0., 1.]])

По умолчанию значения, которые может принимать каждый объект, автоматически выводятся из набора данных и могут быть найдены в categories_ атрибуте:

>>> enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]

Это можно указать явно с помощью параметра categories. В нашем наборе данных есть два пола, четыре возможных континента и четыре веб-браузера:

>>> genders = ['female', 'male']
>>> locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
>>> browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
>>> enc = preprocessing.OneHotEncoder(categories=[genders, locations, browsers])
>>> # Note that for there are missing categorical values for the 2nd and 3rd
>>> # feature
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(categories=[['female', 'male'],
                          ['from Africa', 'from Asia', 'from Europe',
                           'from US'],
                          ['uses Chrome', 'uses Firefox', 'uses IE',
                           'uses Safari']])
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]])

Если есть вероятность, что в обучающих данных могут отсутствовать категориальные особенности, часто бывает лучше указать, handle_unknown='ignore' а не устанавливать categories вручную, как указано выше. Если handle_unknown='ignore' задано значение и во время преобразования встречаются неизвестные категории, ошибка не возникает, но в столбцах с горячим кодированием для этой функции будут все нули ( handle_unknown='ignore' поддерживается только для горячего кодирования):

>>> enc = preprocessing.OneHotEncoder(handle_unknown='ignore')
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(handle_unknown='ignore')
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 0., 0., 0.]])

Также можно кодировать каждый столбец в столбцы n_categories — 1 вместо столбцов n_categories с помощью параметра drop. Этот параметр позволяет пользователю указать категорию для каждой удаляемой функции. Это полезно, чтобы избежать коллинеарности входной матрицы в некоторых классификаторах. Такая функциональность полезна, например, при использовании нерегуляризованной регрессии (LinearRegression), поскольку коллинеарность приведет к тому, что ковариационная матрица будет необратимой. Если этот параметр не равен None, handle_unknown необходимо установить значение error:

>>> X = [['male', 'from US', 'uses Safari'],
...      ['female', 'from Europe', 'uses Firefox']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='first').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 1., 1.],
       [0., 0., 0.]])

Можно удалить один из двух столбцов только для функций с двумя категориями. В этом случае вы можете установить параметр drop='if_binary'.

>>> X = [['male', 'US', 'Safari'],
...      ['female', 'Europe', 'Firefox'],
...      ['female', 'Asia', 'Chrome']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='if_binary').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['Asia', 'Europe', 'US'], dtype=object), array(['Chrome', 'Firefox', 'Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 0., 0., 1., 0., 0., 1.],
       [0., 0., 1., 0., 0., 1., 0.],
       [0., 1., 0., 0., 1., 0., 0.]])

В преобразованном виде $X$ первый столбец представляет собой кодирование признака с категориями «мужской» / «женский», а остальные 6 столбцов — это кодирование 2 признаков с соответственно 3 категориями в каждом.

OneHotEncoder поддерживает категориальные функции с пропущенными значениями, рассматривая отсутствующие значения как дополнительную категорию:

>>> X = [['male', 'Safari'],
...      ['female', None],
...      [np.nan, 'Firefox']]
>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['female', 'male', nan], dtype=object),
 array(['Firefox', 'Safari', None], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0., 1., 0.],
       [1., 0., 0., 0., 0., 1.],
       [0., 0., 1., 1., 0., 0.]])

Если функция содержит оба np.nan и None, они будут считаться отдельными категориями:

>>> X = [['Safari'], [None], [np.nan], ['Firefox']]
>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['Firefox', 'Safari', None, nan], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.],
       [1., 0., 0., 0.]])

См. Раздел Загрузка функций из dicts, чтобы узнать о категориальных функциях, которые представлены как dict, а не как скаляры.

6.3.5. Дискретность

Дискретизация (также известная как квантование или биннинг) обеспечивает способ разделения непрерывных функций на дискретные значения. Определенные наборы данных с непрерывными объектами могут выиграть от дискретизации, потому что дискретизация может преобразовать набор данных с непрерывными атрибутами в набор только с номинальными атрибутами.

Дискретизированные признаки, закодированные одним горячим способом (One-hot encoded), могут сделать модель более выразительной, сохраняя при этом интерпретируемость. Например, предварительная обработка с помощью дискретизатора может внести нелинейность в линейные модели.

6.3.5.1. Дискретизация K-бинов

KBinsDiscretizer дискретизирует функции в k бункеры:

>>> X = np.array([[ -3., 5., 15 ],
...               [  0., 6., 14 ],
...               [  6., 3., 11 ]])
>>> est = preprocessing.KBinsDiscretizer(n_bins=[3, 2, 2], encode='ordinal').fit(X)

По умолчанию выходные данные быстро кодируются в разреженную матрицу (см. Категориальные функции кодирования ), и это можно настроить с помощью encodeпараметра. Для каждого объекта границы fit интервалов вычисляются во время и вместе с количеством интервалов они определяют интервалы. Следовательно, для текущего примера эти интервалы определены как:

• особенность 1: ${[-\infty, -1), [-1, 2), [2, \infty)}$
• особенность 2: ${[-\infty, 5), [5, \infty)}$
• особенность 3: ${[-\infty, 14), [14, \infty)}$

На основе этих интервалов бинов X преобразуется следующим образом:

>>> est.transform(X)                      
array([[ 0., 1., 1.],
       [ 1., 1., 1.],
       [ 2., 0., 0.]])

Результирующий набор данных содержит порядковые атрибуты, которые в дальнейшем можно использовать в файле Pipeline.

Дискретизация аналогична построению гистограмм для непрерывных данных. Однако гистограммы фокусируются на подсчете объектов, которые попадают в определенные интервалы, тогда как дискретизация фокусируется на присвоении значений признаков этим интервалам.

KBinsDiscretizer реализует различные стратегии биннинга, которые можно выбрать с помощью strategy параметра. «Равномерная» стратегия использует ячейки постоянной ширины. Стратегия «квантилей» использует значения квантилей, чтобы иметь одинаково заполненные ячейки в каждой функции. Стратегия «k-средних» определяет интервалы на основе процедуры кластеризации k-средних, выполняемой для каждой функции независимо.

Имейте в виду, что можно указать настраиваемые интервалы, передав вызываемый объект, определяющий стратегию дискретизации FunctionTransformer. Например, мы можем использовать функцию Pandas pandas.cut:

>>> import pandas as pd
>>> import numpy as np
>>> bins = [0, 1, 13, 20, 60, np.inf]
>>> labels = ['infant', 'kid', 'teen', 'adult', 'senior citizen']
>>> transformer = preprocessing.FunctionTransformer(
...     pd.cut, kw_args={'bins': bins, 'labels': labels, 'retbins': False}
... )
>>> X = np.array([0.2, 2, 15, 25, 97])
>>> transformer.fit_transform(X)
['infant', 'kid', 'teen', 'adult', 'senior citizen']
Categories (5, object): ['infant' < 'kid' < 'teen' < 'adult' < 'senior citizen']

6.3.5.2. Бинаризация функций

Бинаризация функций — это процесс определения пороговых значений числовых функций для получения логических значений . Это может быть полезно для последующих вероятностных оценок, которые предполагают, что входные данные распределены согласно многомерному распределению Бернулли . Например, это касается BernoulliRBM.

В сообществе обработки текста также распространено использование двоичных значений признаков (вероятно, для упрощения вероятностных рассуждений), даже если нормализованные подсчеты (также известные как частоты терминов) или функции, оцениваемые по TF-IDF, часто работают немного лучше на практике.

Что касается Normalizer класса утилиты, Binarizer он предназначен для использования на ранних этапах Pipeline. Метод fit не делает ничего , поскольку каждый образец обрабатывают независимо от других:

>>> X = [[ 1., -1.,  2.],
...      [ 2.,  0.,  0.],
...      [ 0.,  1., -1.]]

>>> binarizer = preprocessing.Binarizer().fit(X)  # fit does nothing
>>> binarizer
Binarizer()

>>> binarizer.transform(X)
array([[1., 0., 1.],
       [1., 0., 0.],
       [0., 1., 0.]])

Есть возможность настроить порог бинаризатора:

>>> binarizer = preprocessing.Binarizer(threshold=1.1)
>>> binarizer.transform(X)
array([[0., 0., 1.],
       [1., 0., 0.],
       [0., 0., 0.]])

Что касается Normalizer класса, модуль предварительной обработки предоставляет вспомогательную функцию, binarize которая будет использоваться, когда API-интерфейс преобразователя не нужен.

Обратите внимание, что Binarizer это похоже на то, KBinsDiscretizer когда k = 2 и когда край ячейки находится на значении threshold.

6.3.6. Вменение пропущенных значений

Инструменты для вменения пропущенных значений обсуждаются в разделе «Вменение пропущенных значений» .

6.3.7. Создание полиномиальных признаков

Часто бывает полезно усложнить модель, учитывая нелинейные особенности входных данных. Простой и распространенный метод использования — это полиномиальные функции, которые могут получить термины высокого порядка и взаимодействия функций. Реализован в PolynomialFeatures:

>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

Особенности X были преобразованы из $(X_1, X_2)$ к $(1, X_1, X_2, X_1^2, X_1X_2, X_2^2)$.

В некоторых случаях требуются только условия взаимодействия между функциями, и это можно получить с помощью настройки interaction_only=True:

>>> X = np.arange(9).reshape(3, 3)
>>> X
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
>>> poly = PolynomialFeatures(degree=3, interaction_only=True)
>>> poly.fit_transform(X)
array([[  1.,   0.,   1.,   2.,   0.,   0.,   2.,   0.],
       [  1.,   3.,   4.,   5.,  12.,  15.,  20.,  60.],
       [  1.,   6.,   7.,   8.,  42.,  48.,  56., 336.]])

Особенности $X$ были преобразованы из $(X_1, X_2, X_3)$ к $(1, X_1, X_2, X_3, X_1X_2, X_1X_3, X_2X_3, X_1X_2X_3)$.

Обратите внимание , что полиномиальные функции используются неявно в методах ядра (например, SVC, KernelPCA) при использовании полиномиальных функций ядра .

См. Раздел Полиномиальная интерполяция для регрессии Риджа с использованием созданных полиномиальных функций.

6.3.8. Трансформаторы на заказ

Часто вам может потребоваться преобразовать существующую функцию Python в преобразователь для помощи в очистке или обработке данных. Вы можете реализовать преобразователь из произвольной функции с помощью FunctionTransformer. Например, чтобы создать преобразователь, который применяет преобразование журнала в конвейере, выполните:

>>> import numpy as np
>>> from sklearn.preprocessing import FunctionTransformer
>>> transformer = FunctionTransformer(np.log1p, validate=True)
>>> X = np.array([[0, 1], [2, 3]])
>>> transformer.transform(X)
array([[0.        , 0.69314718],
       [1.09861229, 1.38629436]])

Вы можете убедиться, что func и inverse_func являются противоположностью друг другу, установив check_inverse=True и вызвав fit раньше transform. Обратите внимание, что появляется предупреждение, которое может быть преобразовано в ошибку с помощью filterwarnings:

>>> import warnings
>>> warnings.filterwarnings("error", message=".*check_inverse*.",
...                         category=UserWarning, append=False)

Полный пример кода, демонстрирующий использование a FunctionTransformer для извлечения функций из текстовых данных, см. В разделе Преобразователь столбцов с гетерогенными источниками данных.