6.6. Случайная проекция ¶
В sklearn.random_projection модуле реализован простой и эффективный с точки зрения вычислений способ уменьшить размерность данных путем обмена контролируемой точности (в качестве дополнительной дисперсии) на более быстрое время обработки и меньшие размеры модели. Этот модуль реализует два типа неструктурированных случайных матриц: гауссовскую случайную матрицу и разреженную случайную матрицу.
Размеры и распределение матриц случайных проекций контролируются таким образом, чтобы сохранить попарные расстояния между любыми двумя выборками набора данных. Таким образом, случайная проекция является подходящей аппроксимационной техникой для метода, основанного на расстоянии.
Рекомендации
- Санджой Дасгупта. 2000. Эксперименты со случайной проекцией. В материалах шестнадцатой конференции по неопределенности в искусственном интеллекте (UAI’00), Крейг Бутилье и Мойзес Гольдсмидт (ред.). Морган Кауфманн Паблишерс Инк., Сан-Франциско, Калифорния, США, 143–151.
- Элла Бингхэм и Хейкки Манила. 2001. Случайная проекция в уменьшении размерности: приложения к изображениям и текстовым данным. В материалах седьмой международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных (KDD ’01). ACM, Нью-Йорк, Нью-Йорк, США, 245-250.
6.6.1. Лемма Джонсона-Линденштрауса
Основным теоретическим результатом эффективности случайной проекции является лемма Джонсона-Линденштрауса (цитируется из Википедии) :
В математике лемма Джонсона-Линденштрауса является результатом, касающимся вложений с низким уровнем искажений точек из многомерного евклидова пространства в низкоразмерное евклидово пространство. Лемма утверждает, что небольшой набор точек в пространстве большой размерности может быть вложен в пространство гораздо меньшей размерности таким образом, что расстояния между точками почти сохраняются. Отображение, используемое для вложения, по крайней мере липшицево, и даже может считаться ортогональной проекцией.
Зная только количество выборок, johnson_lindenstrauss_min_dim консервативно оценивается минимальный размер случайного подпространства, чтобы гарантировать ограниченное искажение, вносимое случайной проекцией:
>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim >>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5) 663 >>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01]) array([ 663, 11841, 1112658]) >>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1) array([ 7894, 9868, 11841])
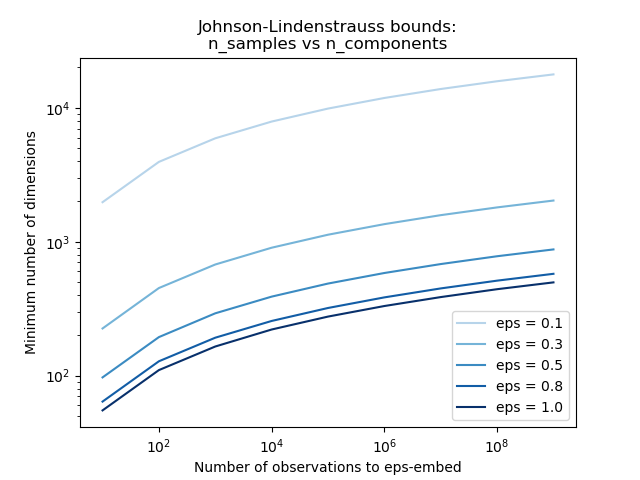
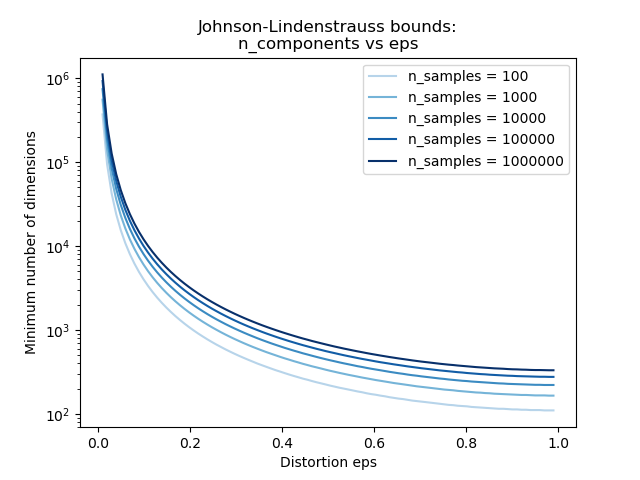
Пример:
- См . Оценку Джонсона-Линденштрауса для вложения со случайными проекциями для теоретического объяснения леммы Джонсона-Линденштрауса и эмпирической проверки с использованием разреженных случайных матриц.
Рекомендации:
- Санджой Дасгупта и Анупам Гупта, 1999. Элементарное доказательство леммы Джонсона-Линденштрауса.
6.6.2. Гауссовская случайная проекция
GaussianRandomProjection Уменьшает размерность путем проецирования исходного входное пространства на случайно сгенерированную матрице , в которой компоненты взяты из следующего распределения $N(0, \frac{1}{n_{components}})$.
Вот небольшой отрывок, который иллюстрирует, как использовать преобразователь случайной проекции Гаусса:
>>> import numpy as np >>> from sklearn import random_projection >>> X = np.random.rand(100, 10000) >>> transformer = random_projection.GaussianRandomProjection() >>> X_new = transformer.fit_transform(X) >>> X_new.shape (100, 3947)
6.6.3. Редкая случайная проекция
SparseRandomProjection Уменьшает размерность путем проецирования исходного входного пространства с помощью разреженной матрицы случайной.
Разреженные случайные матрицы являются альтернативой плотной гауссовской матрице случайных проекций, которая гарантирует аналогичное качество встраивания, но при этом намного эффективнее использует память и позволяет быстрее вычислять проецируемые данные.
Если мы определим s = 1 / density, элементы случайной матрицы взяты из
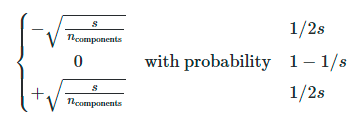
где $n_{\text{components}}$ размер проецируемого подпространства. По умолчанию плотность ненулевых элементов установлена на минимальную плотность, рекомендованную Пинг Ли и др .: $1 / \sqrt{n_{\text{features}}}$.
Вот небольшой отрывок, который иллюстрирует, как использовать преобразователь разреженных случайных проекций:
>>> import numpy as np >>> from sklearn import random_projection >>> X = np.random.rand(100, 10000) >>> transformer = random_projection.SparseRandomProjection() >>> X_new = transformer.fit_transform(X) >>> X_new.shape (100, 3947)
Рекомендации
- Д. Ахлиоптас. 2003. Случайные прогнозы, удобные для баз данных: Джонсон-Линденштраус с бинарными монетами . Журнал компьютерных и системных наук 66 (2003) 671–687
- Пинг Ли, Тревор Дж. Хасти и Кеннет В. Черч. 2006. Очень редкие случайные прогнозы. В материалах 12-й международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных (KDD ’06). ACM, Нью-Йорк, Нью-Йорк, США, 287-296.
