2.1. Модели гауссовой смеси (Gaussian Mixture Model (GMM)) ¶
sklearn.mixture представляет собой пакет, который позволяет изучать модели гауссовой смеси (поддерживаются диагональные, сферические, связанные и полные ковариационные матрицы), отбирать их и оценивать по данным. Также предоставляются средства, помогающие определить подходящее количество компонентов.
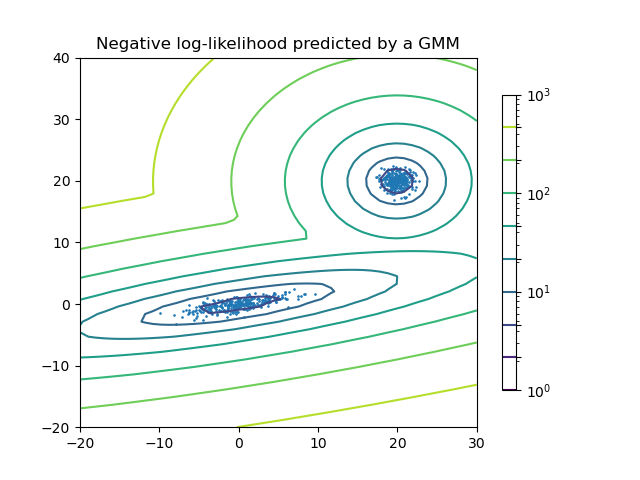
Модель двухкомпонентной гауссовой смеси: точки данных и равновероятные поверхности модели.
Модель смеси Гаусса — это вероятностная модель, которая предполагает, что все точки данных генерируются из смеси конечного числа распределений Гаусса с неизвестными параметрами. Можно думать о смешанных моделях как об обобщении кластеризации k-средних для включения информации о ковариационной структуре данных, а также о центрах скрытых гауссиан.
Scikit-learn реализует разные классы для оценки моделей гауссовой смеси, которые соответствуют различным стратегиям оценки, подробно описанным ниже.
2.1.1. Гауссова смесь (Gaussian Mixture)
В GaussianMixture объект реализует ожидания максимизации (ОМ) алгоритм для установки смеси из-гауссовых-моделей. Он также может рисовать эллипсоиды уверенности для многомерных моделей и вычислять байесовский информационный критерий для оценки количества кластеров в данных. Предоставляется метод GaussianMixture.fit, который изучает модель гауссовой смеси на основе данных обучающей выборки. Учитывая тестовые данные, он может назначить каждому образцу гауссиан, которому он, скорее всего, принадлежит с помощью метода GaussianMixture.predict .
Предлагаются GaussianMixture различные варианты ограничения ковариации оцениваемых классов различий: сферическая, диагональная, связанная или полная ковариация.
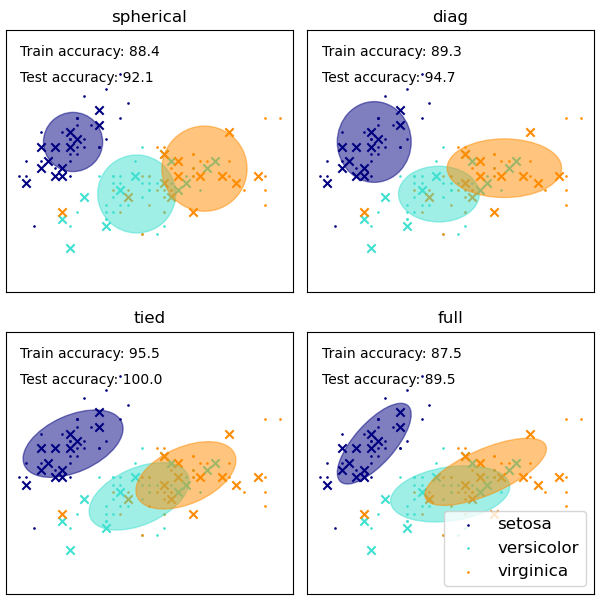
Примеры:
- См. В разделе Ковариации GMM пример использования гауссовой смеси для кластеризации набора данных по радужной оболочке.
- См. В разделе Оценка плотности для гауссовой смеси пример построения графика оценки плотности.
2.1.1.1. Плюсы и минусы класса GaussianMixture
2.1.1.1.1. Плюсы
Скорость Это самый быстрый алгоритм для изучения моделей смесей.
Агностик Поскольку этот алгоритм максимизирует только вероятность, он не будет смещать средние значения к нулю или смещать размеры кластера, чтобы иметь определенные структуры, которые могут или не могут применяться.
2.1.1.1.2. Минусы
Особенности Когда у кого-то недостаточно много точек на смесь, оценка ковариационных матриц становится трудной, и известно, что алгоритм расходится и находит решения с бесконечной вероятностью, если никто не регуляризует ковариации искусственно.
Количество компонентов Этот алгоритм всегда будет использовать все компоненты, к которым у него есть доступ, требуя удерживаемых данных или теоретических критериев информации, чтобы решить, сколько компонентов использовать при отсутствии внешних сигналов.
2.1.1.2. Выбор количества компонентов в классической модели гауссовой смеси
Критерий BIC может использоваться для эффективного выбора количества компонентов в гауссовой смеси. Теоретически он восстанавливает истинное количество компонентов только в асимптотическом режиме (т. Е. Если доступно много данных и предполагается, что данные были фактически сгенерированы iid из смеси гауссовых распределений). Обратите внимание, что использование вариационной байесовской гауссовой смеси позволяет избежать указания количества компонентов для модели гауссовой смеси.
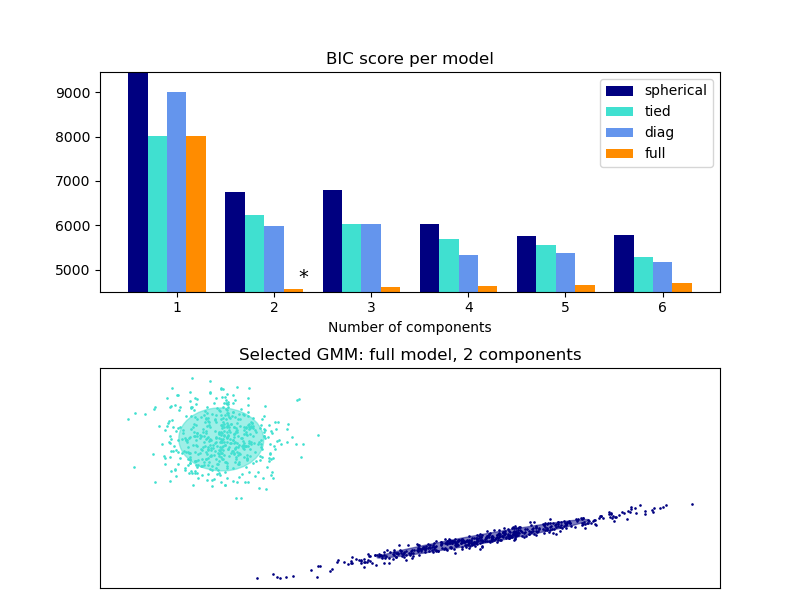
Примеры:
- См. В разделе Выбор модели гауссовой смеси пример выбора модели, выполненный с использованием классической гауссовой смеси.
2.1.1.3. Алгоритм оценки Максимальное ожидание
Основная трудность в изучении моделей гауссовой смеси на основе немаркированных данных заключается в том, что обычно не известно, какие точки были получены из какого скрытого компонента (если у кого-то есть доступ к этой информации, становится очень легко подогнать отдельное гауссово распределение для каждого набора точки). Максимизация ожидания — это хорошо обоснованный статистический алгоритм, позволяющий обойти эту проблему с помощью итеративного процесса. Первый предполагает случайные компоненты (случайным образом центрированные по точкам данных, полученные из k-средних или даже просто нормально распределенные вокруг начала координат) и вычисляет для каждой точки вероятность быть сгенерированной каждым компонентом модели. Затем можно настроить параметры, чтобы максимизировать вероятность данных с учетом этих назначений. Повторение этого процесса гарантирует всегда схождение к локальному оптимуму.
2.1.2. Вариационная байесовская гауссовская смесь
Объект BayesianGaussianMixture реализует вариант гауссовой модели смеси с вариационных алгоритмов логического вывода. API похож на тот, который определен в GaussianMixture.
2.1.2.1. Алгоритм оценки: вариационный вывод
Вариационный вывод — это расширение максимизации ожидания, которое максимизирует нижнюю границу доказательств модели (включая априорные вероятности) вместо вероятности данных. Принцип, лежащий в основе вариационных методов, такой же, как и максимизация ожидания (то есть оба являются итерационными алгоритмами, которые чередуются между нахождением вероятностей для каждой точки, которая должна быть сгенерирована каждой смесью, и подгонкой смеси к этим назначенным точкам), но вариационные методы добавляют регуляризацию с интеграция информации из предыдущих распределений. Это позволяет избежать особенностей, часто встречающихся в решениях максимизации ожидания, но вносит в модель некоторые тонкие искажения. Вывод часто происходит значительно медленнее, но обычно не настолько, чтобы сделать его использование нецелесообразным.
Из-за своей байесовской природы вариационный алгоритм требует больше гиперпараметров, чем максимизация ожидания, наиболее важным из которых является параметр концентрации weight_concentration_prior. Задание низкого значения для предшествующей концентрации заставит модель возложить большую часть веса на несколько компонентов, а веса остальных компонентов будут очень близки к нулю. Высокие значения предварительной концентрации позволят большему количеству компонентов быть активными в смеси.
Реализация класса параметров BayesianGaussianMixture предлагает два типа априора для распределения весов: модель конечной смеси с распределением Дирихле и модель бесконечной смеси с процессом Дирихле. На практике алгоритм вывода процесса Дирихле является приближенным и использует усеченное распределение с фиксированным максимальным числом компонентов (так называемое представление с разрывом прилипания). Количество фактически используемых компонентов почти всегда зависит от данных.
На следующем рисунке сравниваются результаты, полученные для разного типа априорной весовой концентрации (параметра weight_concentration_prior_type) для разных значений weight_concentration_prior. Здесь мы видим, что значение weight_concentration_prior параметра сильно влияет на эффективное количество полученных активных компонентов. Мы также можем заметить, что большие значения для предшествующего веса концентрации приводят к более однородным весам, когда типом Priority является ‘dirichlet_distribution’, в то время как это не обязательно так для типа ‘dirichlet_process’ (используется по умолчанию).
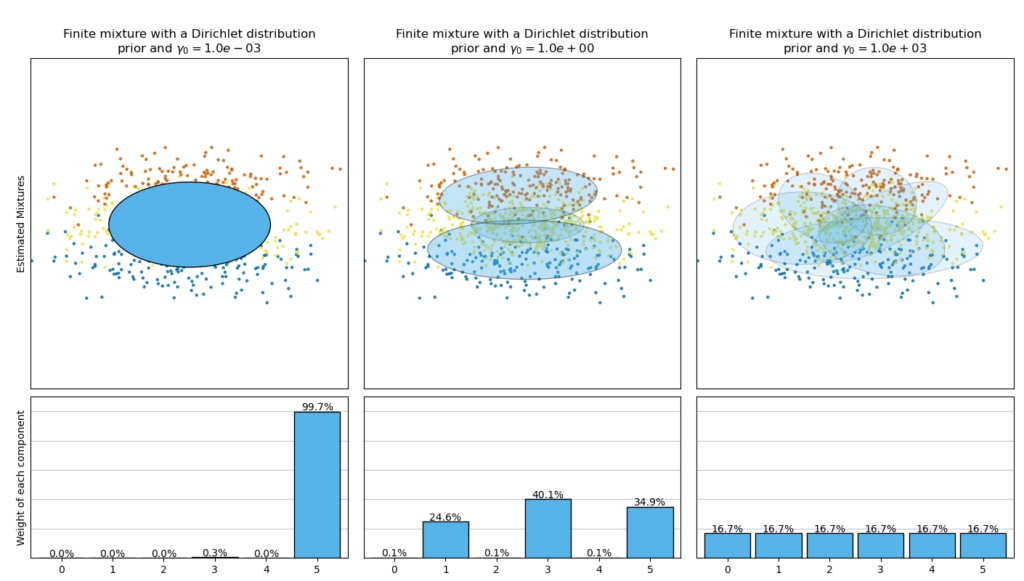
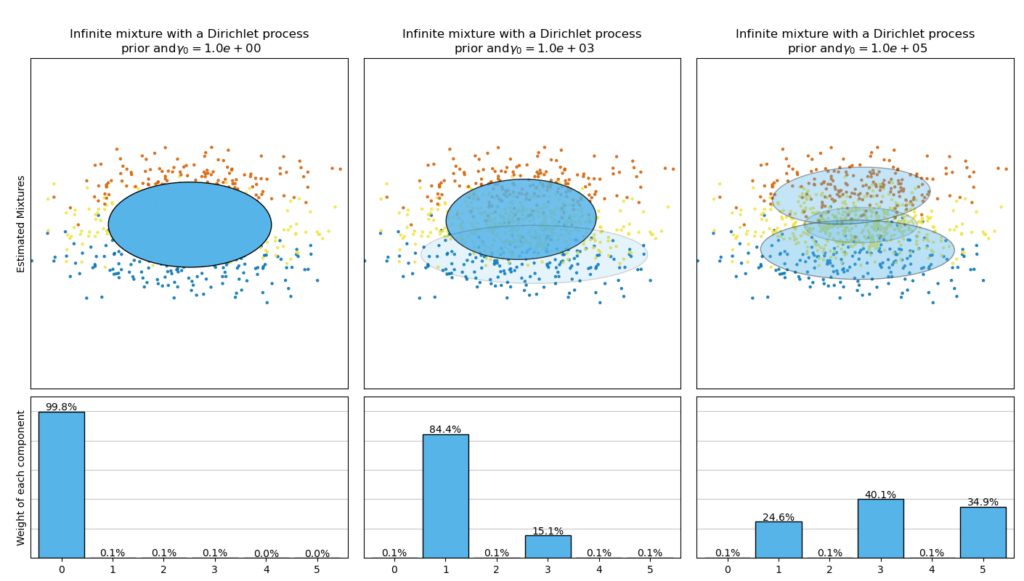
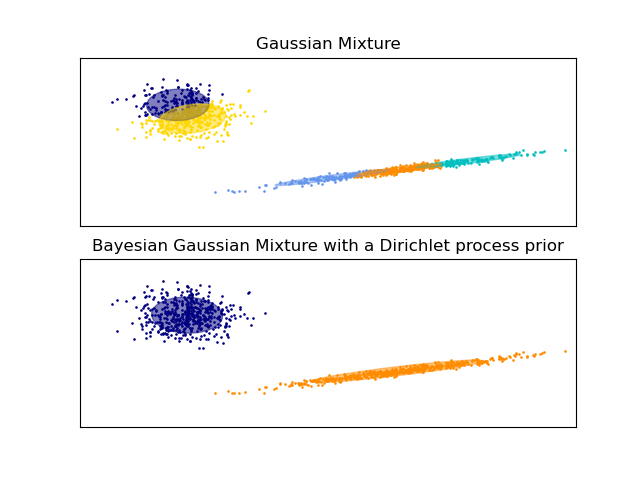
В приведенных ниже примерах сравниваются модели гауссовой смеси с фиксированным числом компонентов с вариационными моделями гауссовой смеси с предшествующим процессом Дирихле. Здесь классическая гауссова смесь соответствует 5 компонентам в наборе данных, состоящем из 2 кластеров. Мы можем видеть, что вариационная гауссовская смесь с предварительным процессом Дирихле может ограничиваться только двумя компонентами, тогда как гауссовская смесь соответствует данным с фиксированным числом компонентов, которое должно быть установлено пользователем априори. В этом случае пользователь выбрал то, n_components=5 что не соответствует истинному генеративному распределению этого набора данных игрушек. Обратите внимание, что при очень небольшом количестве наблюдений вариационные модели гауссовской смеси с априорным процессом Дирихле могут занять консервативную позицию и соответствовать только одному компоненту.
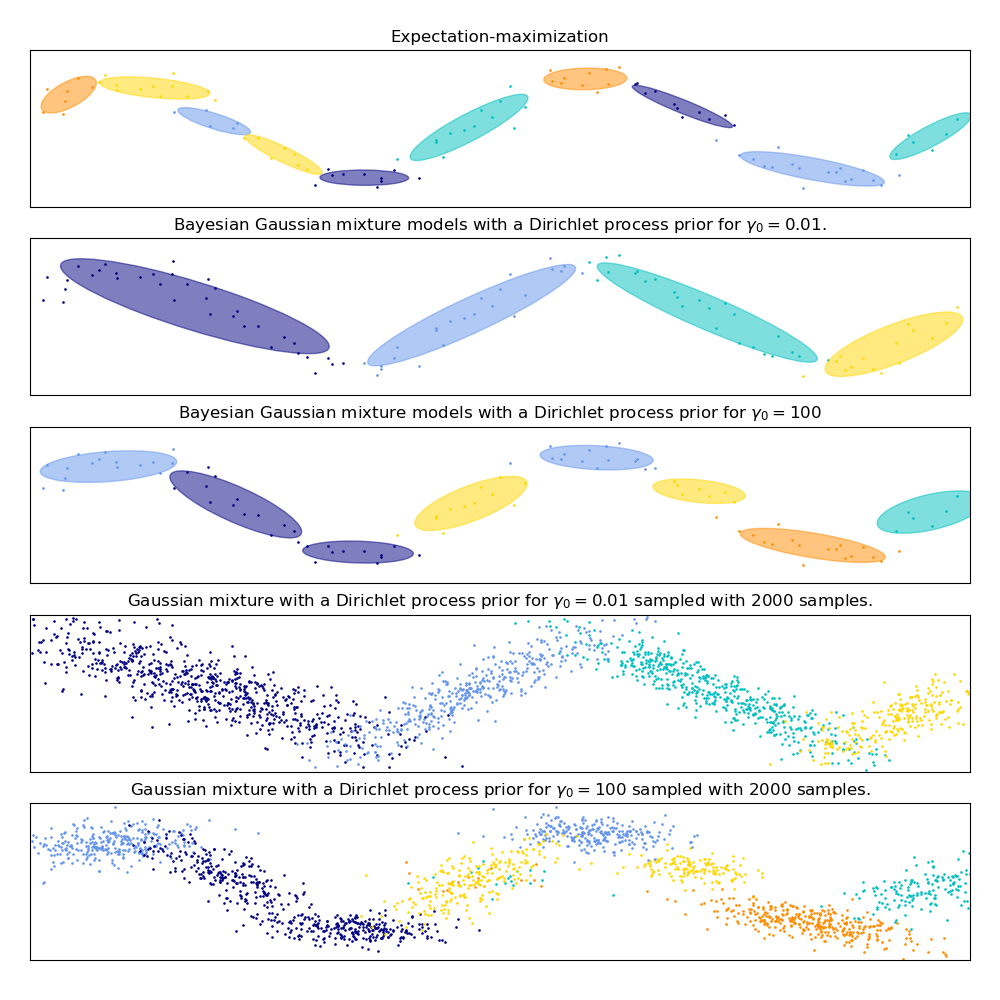
На следующем рисунке мы подбираем набор данных, не очень хорошо отображаемый гауссовой смесью. Регулировка weight_concentration_prior параметра, элементов BayesianGaussianMixture управления количеством компонентов, используемых для соответствия этим данным. Мы также представляем на последних двух графиках случайную выборку, созданную из двух полученных смесей.
Примеры
- См. Пример построения эллипсоидов доверительной вероятности для обоих и в разделе Эллипсоиды модели гауссовой смеси .
GaussianMixture иBayesianGaussianMixture - Синусоидальная кривая модели гауссовой смеси показывает использование
GaussianMixtureиBayesianGaussianMixtureподгонку синусоидальной волны. - См концентрации перед Тип Анализ вариации байесовской гауссовой смеси для примера построения доверительных эллипсоидов для
BayesianGaussianMixtureс различнымиweight_concentration_prior_typeдля различных значений параметраweight_concentration_prior.
2.1.2.2. Плюсы и минусы вариационного вывода с BayesianGaussianMixture
2.1.2.2.1. Плюсы
Автоматический выбор когда weight_concentration_prior достаточно мало и n_components больше, чем это необходимо для модели, модель вариационной байесовской смеси имеет естественную тенденцию устанавливать некоторые значения весов смеси близкими к нулю. Это позволяет модели автоматически выбирать подходящее количество эффективных компонентов. Необходимо указать только верхнюю границу этого числа. Однако обратите внимание, что «идеальное» количество активных компонентов очень зависит от приложения и обычно плохо определяется в настройках исследования данных.
Меньшая чувствительность к количеству параметров в отличие от конечных моделей, которые почти всегда будут использовать все компоненты в максимально возможной степени и, следовательно, будут давать совершенно разные решения для разного количества компонентов, вариационный вывод с помощью процесса Дирихле Prior ( weight_concentration_prior_type='dirichlet_process') не будет сильно меняться при изменении параметров , что приводит к большей стабильности и меньшему количеству настроек.
Регуляризация из-за включения априорной информации вариационные решения имеют меньше патологических частных случаев, чем решения с максимизацией ожидания.
2.1.2.2.2. Минусы
Скорость дополнительная параметризация, необходимая для вариационного вывода, делает вывод медленнее, хотя и ненамного.
Гиперпараметры этому алгоритму нужен дополнительный гиперпараметр, который может потребовать экспериментальной настройки с помощью перекрестной проверки.
Предвзятость есть много неявных смещений в алгоритмах вывода (а также в процессе Дирихле, если он используется), и всякий раз, когда есть несоответствие между этими смещениями и данными, можно подобрать лучшие модели, используя конечную смесь.
2.1.2.3. Процесс Дирихле
Здесь мы описываем вариационные алгоритмы вывода на смеси процессов Дирихле. Процесс Дирихле — это априорное распределение вероятностей для кластеризации с бесконечным неограниченным числом разбиений . Вариационные методы позволяют нам включить эту априорную структуру в модели гауссовой смеси практически без потери времени вывода по сравнению с моделью конечной гауссовой смеси.
Важный вопрос заключается в том, как процесс Дирихле может использовать бесконечное неограниченное число кластеров и при этом быть согласованным. Хотя полное объяснение не подходит для этого руководства, можно подумать о процессе разрушения палки аналогия, чтобы помочь понять это. Процесс разрушения палки — это генеративная история для процесса Дирихле. Мы начинаем с палки единичной длины и на каждом шаге отламываем часть оставшейся палки. Каждый раз мы связываем длину кусочка палки с долей точек, которые попадают в группу смеси. В конце, чтобы представить бесконечную смесь, мы связываем последний оставшийся кусок палки с долей точек, которые не попадают во все другие группы. Длина каждого кусочка является случайной величиной с вероятностью, пропорциональной параметру концентрации. Меньшее значение концентрации разделит единицу длины на более крупные части палочки (определяя более концентрированное распределение).Более высокие значения концентрации создадут меньшие части палочки (увеличивая количество компонентов с ненулевым весом).
Методы вариационного вывода для процесса Дирихле по-прежнему работают с конечным приближением к этой модели бесконечной смеси, но вместо того, чтобы заранее указывать, сколько компонентов нужно использовать, нужно просто указать параметр концентрации и верхнюю границу количества смеси. компонентов (эта верхняя граница, если предположить, что она превышает «истинное» количество компонентов, влияет только на алгоритмическую сложность, а не на фактическое количество используемых компонентов).
