4.1. Графики частичной зависимости и индивидуальных условных ожиданий ¶

Графики частичной зависимости (PDP) и графики индивидуального условного ожидания (ICE) могут использоваться для визуализации и анализа взаимодействия между целевым ответом 1 и набором входных характеристик, представляющих интерес.

И PDP, и ICE предполагают, что интересующие входные функции не зависят от дополнительных функций, и это предположение часто нарушается на практике. Таким образом, в случае коррелированных функций мы создадим абсурдные точки данных для вычисления PDP / ICE.

4.1.1. Графики частичной зависимости

Графики частичной зависимости (PDP) показывают зависимость между целевым ответом и набором представляющих интерес входных характеристик, уступая значениям всех других входных характеристик («дополнительные» функции). Интуитивно мы можем интерпретировать частичную зависимость как ожидаемую целевую реакцию как функцию интересующих входных характеристик.

Из-за ограничений человеческого восприятия размер набора представляющих интерес входных характеристик должен быть небольшим (обычно один или два), поэтому интересующие входные характеристики обычно выбираются среди наиболее важных.

На рисунке ниже показаны два односторонних и один двусторонний график частичной зависимости для набора данных по жилищному строительству Калифорнии с HistGradientBoostingRegressor:

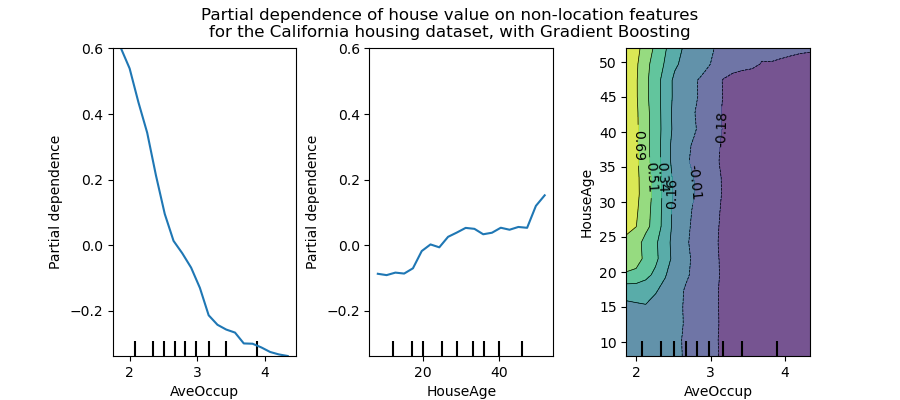
Односторонние PDP рассказывают нам о взаимодействии между целевым ответом и входной функцией, представляющей интерес (например, линейной, нелинейной). Левый график на приведенном выше рисунке показывает влияние средней заполняемости на среднюю цену дома; мы можем четко видеть линейную зависимость между ними, когда средняя заполняемость меньше 3 человек. Точно так же мы могли бы проанализировать влияние возраста дома на среднюю цену дома (средний участок). Таким образом, эти интерпретации являются маргинальными, учитывая особенности за раз.

PDP с двумя интересующими входными функциями показывают взаимодействие между двумя функциями. Например, PDP с двумя переменными на приведенном выше рисунке показывает зависимость медианной цены дома от совместных значений возраста дома и среднего числа жителей на одно домохозяйство. Мы можем ясно видеть взаимодействие между этими двумя характеристиками: для средней заполняемости больше двух цена дома почти не зависит от возраста дома, тогда как для значений меньше 2 существует сильная зависимость от возраста.

Модуль sklearn.inspection обеспечивает удобную функцию plot_partial_dependence, чтобы создать односторонний и двухсторонний частичные зависимость участков. В приведенном ниже примере мы показываем, как создать сетку графиков частичной зависимости: два односторонних PDP для функций 0 и 1 двусторонний PDP между двумя функциями:

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import plot_partial_dependence

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> plot_partial_dependence(clf, X, features) 

Вы можете получить доступ к вновь созданным объектам Figure и Axes, используя plt.gcf() и plt.gca().

Для мультиклассовой классификации вам необходимо установить метку класса, для которого должны быть созданы PDP, с помощью target аргумента:

>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10,
...     max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> plot_partial_dependence(mc_clf, X, features, target=0) 

Этот же параметр targetиспользуется для указания цели в настройках регрессии с несколькими выходами.

Если вам нужны необработанные значения функции частичной зависимости, а не графики, вы можете использовать функцию sklearn.inspection.partial_dependence :

>>> from sklearn.inspection import partial_dependence

>>> pdp, axes = partial_dependence(clf, X, [0])
>>> pdp
array([[ 2.466...,  2.466..., ...
>>> axes
[array([-1.624..., -1.592..., ...

Значения, при которых следует оценивать частичную зависимость, непосредственно генерируются из X. Для двусторонней частичной зависимости создается 2D-сетка значений. Поле values возвращаемый sklearn.inspection.partial_dependence дает фактические значения , используемые в сетке для каждого входного признака интереса. Они также соответствуют оси графиков.

4.1.2. График индивидуального условного ожидания (ICE)

Подобно PDP, график индивидуального условного ожидания (ICE) показывает зависимость между целевой функцией и входной функцией, представляющей интерес. Однако, в отличие от PDP, который показывает средний эффект входной характеристики, график ICE визуализирует зависимость прогноза от характеристики для каждой выборки отдельно с одной строкой на выборку. Из-за ограничений человеческого восприятия для графиков ICE поддерживается только одна представляющая интерес входная функция.

На рисунках ниже показаны четыре графика ICE для набора данных о жилищном строительстве Калифорнии с расширением HistGradientBoostingRegressor. На втором рисунке изображена соответствующая линия частичного разряда, наложенная на линии ICE.

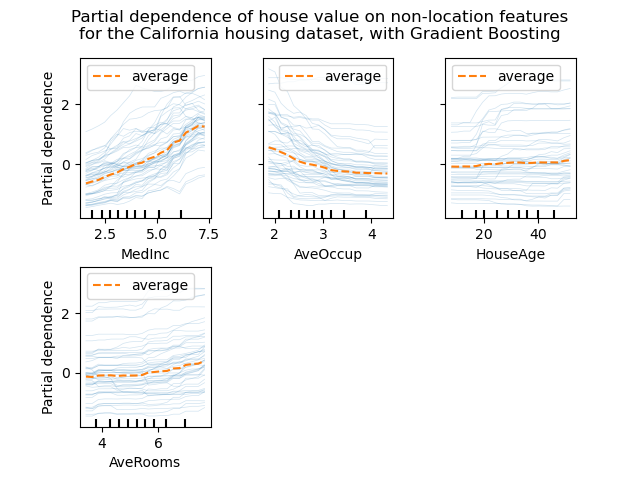
Хотя PDP хорошо показывают средний эффект целевых функций, они могут скрыть гетерогенные отношения, созданные взаимодействиями. При наличии взаимодействий график ICE предоставит гораздо больше информации. Например, мы можем наблюдать линейную зависимость между средним доходом и ценой дома в линии PD. Однако линии ICE показывают, что есть некоторые исключения, когда цена дома остается постоянной в некоторых диапазонах среднего дохода.

В модуле sklearn.inspection plot_partial_dependence удобной функция может быть использована для создания ICE участков путем установкой kind='individual'. В приведенном ниже примере мы показываем, как создать сетку графиков ICE:

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import plot_partial_dependence

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1]
>>> plot_partial_dependence(clf, X, features,
...     kind='individual') 

На графиках ICE может быть непросто увидеть средний эффект интересующей входной характеристики. Следовательно, рекомендуется использовать графики ICE вместе с PDP. Их можно строить вместе с kind='both'.

>>> plot_partial_dependence(clf, X, features,
...     kind='both')  

4.1.3. Математическое определение

Пусть $X_S$- набор входных характеристик, представляющих интерес (т.е. параметр features ), и пусть $X_C$ его дополнение.

Частичная зависимость ответа $f$ в какой-то момент $x_S$ определяется как:
$$\begin{split}pd_{X_S}(x_S) &\overset{def}{=} \mathbb{E}_{X_C}\left[ f(x_S, X_C) \right]\ &= \int f(x_S, x_C) p(x_C) dx_C,\end{split}$$

где $f(x_S,x_C)$ это функция отклика (predict, predict_proba или decision_function) для данного образца, значение которого определяется $x_S$ для функций в $X_S$, и по $x_C$ для функций в $X_C$. Обратите внимание, что $x_S$ а также $x_C$ могут быть кортежами.

Вычисляя этот интеграл для различных значений $x_S$ создает график PDP, как указано выше. Линия ICE определяется как одиночная $f(x_S,x_C^{(i)})$ оценивается в $x_S$.

4.1.4. Методы вычислений

Существует два основных метода аппроксимации указанного выше интеграла, а именно «грубый» и «рекурсивный» методы. В параметре method контролирует  какой метод использовать.

«Грубый» метод — это общий метод, который работает с любым оценщиком. Обратите внимание, что вычисление графиков ICE поддерживается только «грубым» методом. Он аппроксимирует вышеуказанный интеграл, вычисляя среднее значение по данным X:
$$pd_{X_S}(x_S) \approx \frac{1}{n_\text{samples}} \sum_{i=1}^n f(x_S, x_C^{(i)}),$$

где $x_C^{(i)}$ — значение i-й выборки для признаков в $X_C$. Для каждого значения $x_S$, этот метод требует полного прохождения по набору данных, X что требует больших вычислительных ресурсов.

Каждый из $f(x_S,x_C^{(i)})$ соответствует одной линии ICE, оцененной на $x_S$. Вычисляя это для нескольких значений $x_S$, получается полная линия ДВС. Как видно, среднее значение линий ICE соответствует частичной линии зависимости.

Метод «рекурсии» быстрее, чем «грубый» метод, но он поддерживается только для графиков PDP некоторыми древовидными оценщиками. Он рассчитывается следующим образом. Для данной точкиxSвыполняется взвешенный обход дерева: если разделенный узел включает интересующий входной объект, выполняется соответствующая левая или правая ветвь; в противном случае следуют обе ветви, каждая ветвь взвешивается по той части обучающих выборок, которая вошла в эту ветвь. Наконец, частичная зависимость дается средневзвешенным значением всех посещенных листьев.

При «грубом» методе параметр X используется как для генерации сетки значений $x_S$ и значения дополнительных функций $x_C$. Однако с методом «рекурсии» X используется только для значений сетки: неявно $x_C$ значения — это значения обучающих данных.

По умолчанию метод «рекурсии» используется для построения PDP на основе древовидных оценщиков, которые его поддерживают, а для остальных используется «грубый».