6.7. Аппроксимация ядра

Этот подмодуль содержит функции, которые аппроксимируют сопоставления функций, соответствующие определенным ядрам, поскольку они используются, например, в методе опорных векторов (см. Метод опорных векторов ). Следующие функции функций выполняют нелинейные преобразования входных данных, которые могут служить основой для линейной классификации или других алгоритмов.

Преимущество использования приблизительных явных карт функций по сравнению с трюком с ядром , который неявно использует карты функций, состоит в том, что явные сопоставления могут лучше подходить для онлайн-обучения и могут значительно снизить стоимость обучения с очень большими наборами данных. Стандартные ядерные SVM плохо масштабируются для больших наборов данных, но, используя приблизительную карту ядра, можно использовать гораздо более эффективные линейные SVM. В частности, сочетание аппроксимации карты ядра с SGDClassifier может сделать возможным нелинейное обучение на больших наборах данных.

Поскольку не было большого количества эмпирических исследований с использованием приближенных вложений, рекомендуется по возможности сравнивать результаты с точными методами ядра.

Смотрите также

Полиномиальная регрессия: расширение линейных моделей базисными функциями для точного полиномиального преобразования.

6.7.1. Метод Нистроэма для аппроксимации ядра

Метод Nystroem, реализованный в, Nystroem является общим методом для низкоранговых приближений ядер. Это достигается за счет субдискретизации данных, на которых оценивается ядро. По умолчанию Nystroem использует rbf ядро, но может использовать любую функцию ядра или предварительно вычисленную матрицу ядра. Число использованных выборок, которое также является размерностью вычисленных функций, задается параметром n_components.

6.7.2. Ядро радиальной базисной функции

RBFSampler Строит приближенное отображение для радиальной базисной функции ядра, также известный как случайных кухонные раковины [RR2007] . Это преобразование можно использовать для явного моделирования карты ядра перед применением линейного алгоритма, например линейной SVM:

>>> from sklearn.kernel_approximation import RBFSampler
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> rbf_feature = RBFSampler(gamma=1, random_state=1)
>>> X_features = rbf_feature.fit_transform(X)
>>> clf = SGDClassifier(max_iter=5)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=5)
>>> clf.score(X_features, y)
1.0

Отображение основывается на приближении Монте-Карло к значениям ядра. В fit функции выполняет выборки Монте-Карло, в то время как transform метод выполняет отображение данных. Из-за присущей процессу случайности результаты могут различаться между разными вызовами fit функции.

Функция fit принимает два аргумента: n_components, что является целевой мерность функции преобразования и gamma, в параметр RBF-ядра. Более высокое значение n_components приведет к лучшему приближению ядра и приведет к результатам, более похожим на результаты, полученные с помощью SVM ядра. Обратите внимание, что «подгонка» функции функции на самом деле не зависит от данных, передаваемых fit функции. Используется только размерность данных. Подробную информацию о методе можно найти в [RR2007] .

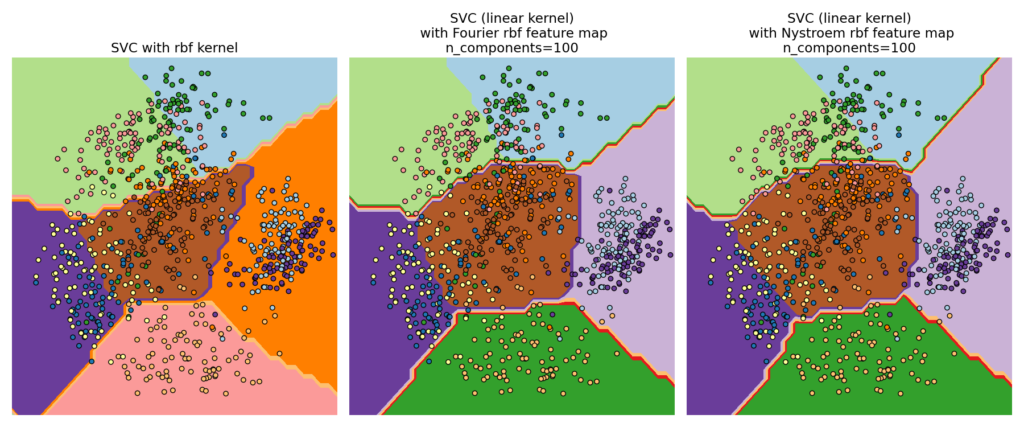
Для данного значения n_components RBFSampler часто менее точен, чем Nystroem. RBFSampler однако дешевле в вычислении, что позволяет более эффективно использовать большие пространства функций.

Сравнение точного ядра RBF (слева) с приближением (справа)

Примеры:

6.7.3. Аддитивное ядро ​​хи-квадрат

Аддитивное ядро ​​хи-квадрат — это ядро ​​на гистограммах, часто используемое в компьютерном зрении.

Используемое здесь аддитивное ядро ​​хи-квадрат дается выражением
$$k(x, y) = \sum_i \frac{2x_iy_i}{x_i+y_i}$$

Это не совсем то же самое sklearn.metrics.additive_chi2_kernel. Авторы [VZ2010] предпочитают версию выше, поскольку она всегда положительно определена. Поскольку ядро ​​аддитивное, можно обрабатывать все компонентыxiотдельно для встраивания. Это позволяет выполнять выборку преобразования Фурье через равные промежутки времени вместо аппроксимации с использованием выборки Монте-Карло.

Класс AdditiveChi2Sampler реализует эту компонентную детерминированную выборку. Каждый компонент отбирается $n$ раз, уступая $2n+1$ измерений на входное измерение (кратное двум происходит от действительной и комплексной части преобразования Фурье). В литературе,nобычно выбирается 1 или 2, преобразуя набор данных в размер n_samples * 5 * n_features (в случае $n= 2$).

Приблизительная карта характеристик, предоставленная компанией, AdditiveChi2Sampler может быть объединена с приблизительной картой характеристик, предоставленной, RBFSampler чтобы получить приблизительную карту характеристик для экспоненциального ядра хи-квадрат. См. [VZ2010] для получения подробной информации и [VVZ2010] для комбинации с RBFSampler.

6.7.4. Ядро с перекосом ци в квадрате

Перекошенное ядро ​​хи-квадрат определяется по формуле:
$$k(x,y) = \prod_i \frac{2\sqrt{x_i+c}\sqrt{y_i+c}}{x_i + y_i + 2c}$$

Он имеет свойства, похожие на экспоненциальное ядро ​​хи-квадрат, часто используемое в компьютерном зрении, но допускает простую аппроксимацию Монте-Карло карты признаков.

Использование класса SkewedChi2Sampler аналогично использованию, описанному выше для RBFSampler. Единственное отличие состоит в свободном параметре, который называетсяc. О мотивации для этого сопоставления и математических подробностях см. [LS2010] .

6.7.5. Аппроксимация полиномиального ядра с помощью тензорного эскиза

Полиномиальное ядро является популярным типом функции ядра определяется по формуле:
$$k(x, y) = (\gamma x^\top y +c_0)^d$$
где:

  • x, y являются входными векторами
  • d степень ядра

Интуитивно понятно, что пространство признаков полиномиального ядра степени d состоит из всех возможных степеней — d произведений среди входных функций, что позволяет алгоритмам обучения, использующим это ядро, учитывать взаимодействия между функциями.

Метод TensorSketch [PP2013] , реализованный в PolynomialCountSketch, представляет собой масштабируемый, независимый от входных данных метод для аппроксимации полиномиального ядра. Он основан на концепции скетча подсчета [WIKICS] [CCF2002] , метода уменьшения размерности, аналогичного хешированию функций, который вместо этого использует несколько независимых хеш-функций. TensorSketch получает эскиз счета внешнего произведения двух векторов (или вектора с самим собой), который можно использовать в качестве аппроксимации пространства признаков полиномиального ядра. В частности, вместо того, чтобы явно вычислять внешний продукт, TensorSketch вычисляет эскиз счета векторов, а затем использует полиномиальное умножение с помощью быстрого преобразования Фурье для вычисления эскиза счета своего внешнего продукта.

Удобно, что этап обучения TensorSketch просто состоит из инициализации некоторых случайных величин. Таким образом, он не зависит от входных данных, то есть зависит только от количества входных функций, но не от значений данных. Кроме того, этот метод может преобразовывать образцы в $\mathcal{O}(n_{\text{samples}}(n_{\text{features}} + n_{\text{components}} \log(n_{\text{components}})))$ время, где $n_{\text{components}}$ — желаемый выходной размер, определяемый n_components.

Примеры:

6.7.6. Математические детали

Такие методы ядра, как поддержка векторных машин или ядерный PCA, полагаются на свойство воспроизведения гильбертовых пространств ядра. Для любой положительно определенной функции ядра $k$ (так называемое ядро ​​Мерсера) гарантировано, что существует отображение $\phi$ в гильбертово пространство $\mathcal{H}$, так что
$$k(x,y) = \langle \phi(x), \phi(y) \rangle$$

Где $\langle \cdot, \cdot \rangle$ обозначает скалярное произведение в гильбертовом пространстве.

Если алгоритм, такой как линейная машина опорных векторов или PCA, полагается только на скалярное произведение точек данных $x_i$, можно использовать значение $k(x_i, x_j)$, что соответствует применению алгоритма к отображенным точкам данных $\phi(x_i)$. Преимущество использования $k$ в том, что отображение $\phi$ никогда не нужно рассчитывать явно, учитывая произвольные большие функции (даже бесконечные).

Одним из недостатков методов ядра является то, что может потребоваться хранить много значений ядра. $k(x_i, x_j)$ во время оптимизации. Если к новым данным применяется ядерный классификатор $y_j$, $k(x_i, y_j)$ необходимо вычислить, чтобы делать прогнозы, возможно, для многих различных $x_i$ в обучающем наборе.

Классы в этом подмодуле позволяют аппроксимировать вложение $\phi$, тем самым явно работая с представлениями $\phi(x_i)$, что избавляет от необходимости применять ядро ​​или хранить обучающие примеры.

Рекомендации: